Χρήση κάμερας για τον υπολογισμό της θέσης

Μέχρι τώρα, μας έχει απασχολήσει σε προηγούμενα άρθρα ο εντοπισμός και η εκτίμηση της θέσης αντικειμένων με χρήση ηλεκτρομαγνητικών και ακουστικών σημάτων.

Όλα ξεκίνησαν από εδώ, όπου προβληματιστήκαμε για το πώς μπορεί να λειτουργεί το GPS.

Ένας άλλος τρόπος για να καταλήξουμε να εκτιμήσουμε τη θέση ενός αντικειμένου στον χώρο όμως είναι με τη βοήθεια καμερών και οπτικών τεχνολογιών.

Ο κύριος περιοριστικός παράγοντας σε αυτές τις προσεγγίσεις είναι η ανάγκη για οπτική επαφή με το αντικείμενο ενδιαφέροντος.

Σε αυτή την περίπτωση, πρακτικά μιλάμε για εφαρμογές Computer Vision, και είναι μία από τις τεχνικές που χρησιμοποιούν αυτόνομα αμάξια και drone για να κατανοήσουν τη θέση τους στον χώρο, ρομπότ για να εντοπίσουν τα αντικείμενα γύρω τους ή ακόμα και στις ταινίες του Hollywood, προκειμένου να καταγράψουν τις κινήσεις των ηθοποιών και να τις μετατρέψουν σε CGI.

Επιπλέον, καταλήγει να είναι και ο τρόπος με τις μεγαλύτερες ανάγκες επεξεργασίας, αφού μιλάμε για ψηφιακή επεξεργασία.

Δεν κάνουμε εμείς τους υπολογισμούς αλλά οι συσκευές… Έτσι δεν είναι..;

Οι περισσότερες κάμερες που χρησιμοποιούμε καθημερινά, αναπαριστούν τον 3D χώρο σε ένα δισδιάστατο επίπεδο που ονομάζεται image plane.

Υπάρχουν, βέβαια, κάποιες εξαιρέσεις, όπως οι RGB-D κάμερες, οι οποίες, εκτός από το color information, παρέχουν και depth πληροφορία για κάθε pixel τους.

Βασικοί τρόποι απόκτησης 3D πληροφορίας – με χρήση 2D που προσφέρει τυπικά μία κάμερα – είναι μέσω των τεχνικών που θα αναλύσουμε σε αυτό το post.

📷 Κάμερες

Στην πραγματικότητα, όταν μιλάμε για εικόνες, ουσιαστικά αναφερόμαστε σε συναρτήσεις που έχουν ως πεδίο ορισμού τα 3D σημεία του χώρου στον οποίο τις λάβαμε, και ως πεδίο τιμών τα 2D projection points που κατέγραψε ο αισθητήρας της κάμερας. Για το projection υπάρχουν διάφορα μοντέλα, όπως το Perspective, το Weak και το Orthographic.

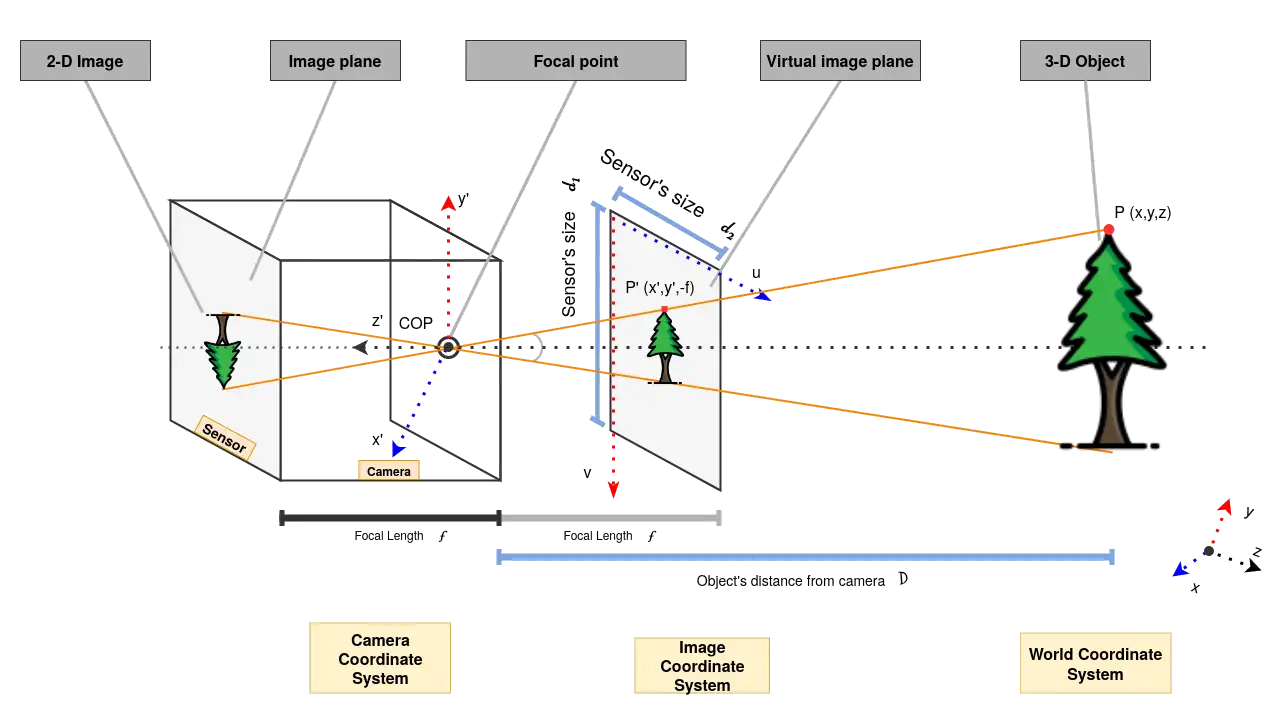
Επίσης, ένα απλό (για την κάμερα) – παρόλα αυτά αρκετά περιγραφικό και κοντά στην πραγματικότητα – μοντέλο, το οποίο χρησιμοποιείται συχνά για εφαρμογές του Computer Vision (CV), είναι αυτό του Pinhole Model. Στην παραπάνω εικόνα το COP αναπαριστά το Center of Projection και χρησιμοποιούμε το Virtual Image Plane για τους υπολογισμούς.

Το Virtual Image Plane είναι μαθηματικά ισοδύναμο με το πραγματικό Image Plane, με τη διαφορά ότι το ειδώλιο δεν είναι ανεστραμμένο.

Θα μπούμε λίγο σε μαθηματικά, αλλά μην τα πολύ σκεφτείς σε αυτή την φάση… Απλά dive in ;)

Μπορούμε να μεταφερθούμε από το World Coordinate System (κοινό σε όλους) \(({}^{w}\overrightarrow{p})\) στο Coordinate System της κάμερας \(({}^{c}\overrightarrow{p})\) μέσω μίας διαδικασίας Rotation \(({}^{c}_{w}R)\) και μίας Translation \(({}^{c}_{w}\overrightarrow{t})\).

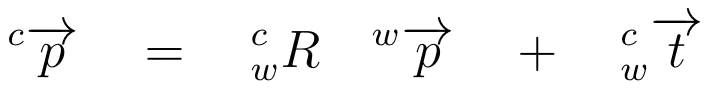
Συχνά, τα περιεχόμενα της Rotation και της Translation ονομάζονται από κοινού Extrinsic Parameters.

Ενώ για τη πραγματική μεταφορά από το Camera Coordinate System σε αυτό της εικόνας, θα πρέπει να λάβουμε υπόψη τις φυσικές παραμέτρους της κάμερας, όπως το Focal Length, το Skew, κ.λπ., οι οποίες συνολικά ονομάζονται Intrinsic Parameters.

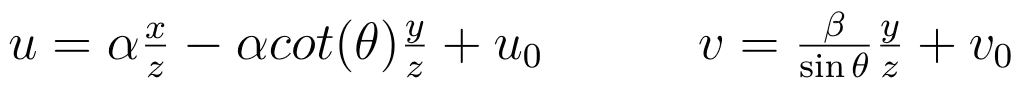
Η σχέση αυτή παρουσιάζει αυτόν τον μετασχηματισμό, με \((u,v)\) τα pixels στην εικόνα, \((x,y,z)\) τις συντεταγμένες του αντικειμένου με βάση το Camera Coordinate System και \((α,β,θ,u0,v0)\) τα Intrinsic Parameters.

Οι παραπάνω υπολογισμοί, με τη μορφή που έχουν αυτήν τη στιγμή, καθιστούν τη διαδικασία υπολογισμού σε ψηφιακά συστήματα πιο δύσκολη. Επιπλέον, περιέχουν μη γραμμικά μέρη, με αποτέλεσμα να μην είναι αναστρέψιμοι. Για αυτόν τον λόγο, γίνεται αναφορά στα homogeneous coordinates.

Τα homogeneous coordinates χρησιμοποιούνται ώστε να μπορούμε να μετασχηματίσουμε εύκολα, σε μία ενιαία μορφή, τις παραπάνω σχέσεις, με χρήση πινάκων.

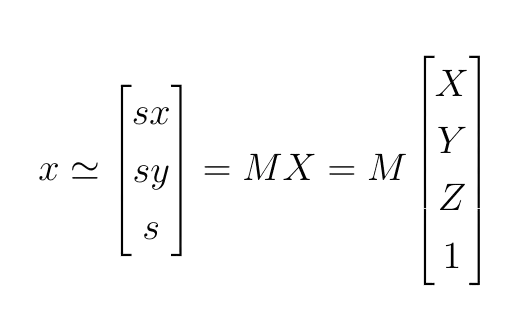
Οπου x οι συντεταγμένες στην εικόνα, X οι συντεταγμένες στον φυσικό κόσμο και M ο πίνακας μετασχηματισμού, τα περιεχόμενα του οποίου αναλύονται στην σε αυτή την σχέση.

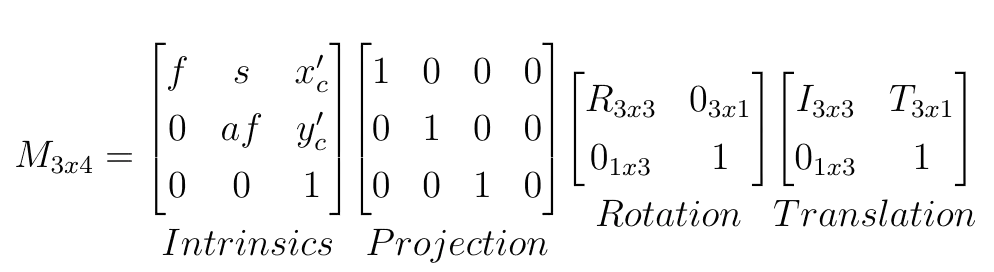
Τι μας λέει αυτή;

Ας κρατήσουμε ένα πράγμα…

Απλά ότι, από τον πραγματικό κόσμο, μέσω μίας γραμμικής σχέσης και χρήσης πινάκων, με δεδομένες τις παραμέτρους της κάμερας (χαρακτηριστικά φακού, θέση της κάμερας κλπ.), αν ξέρουμε τις συντεταγμένες σε pixel ενός αντικειμένου στο image plane, τελικά μπορούμε να βρούμε στο τρισδιάστατο χώρο τις συντεταγμένες του.

Ας πάμε, όμως, σε λίγο πιο απτά παραδείγματα αυτού.

🗼 Structure from Reference

Τυπικά, κατά τη μεταφορά των σημείων του πραγματικού κόσμου 3D σε pixel μιας εικόνας 2D, χάνουμε τη διάσταση του βάθους, πράγμα που μπορεί να δημιουργήσει πλάνες/αυταπάτες.

Ένας τρόπος για την ανάκτηση της πληροφορίας του βάθους – προκειμένου να εκτιμήσουμε μέσω της εικόνας τη θέση των αντικειμένων – είναι να υπάρχουν στην σκηνή μας αντικείμενα γνωστών διαστάσεων, τα οποία θα χρησιμοποιηθούν ως σημεία αναφοράς.

Στην παρακάτω εικόνα παρουσιάζονται οι νοητές ευθείες πορείας του φωτός στο thin lens model, από τα σημεία του τρισδιάστατου κόσμου προς τον αισθητήρα της κάμερας.

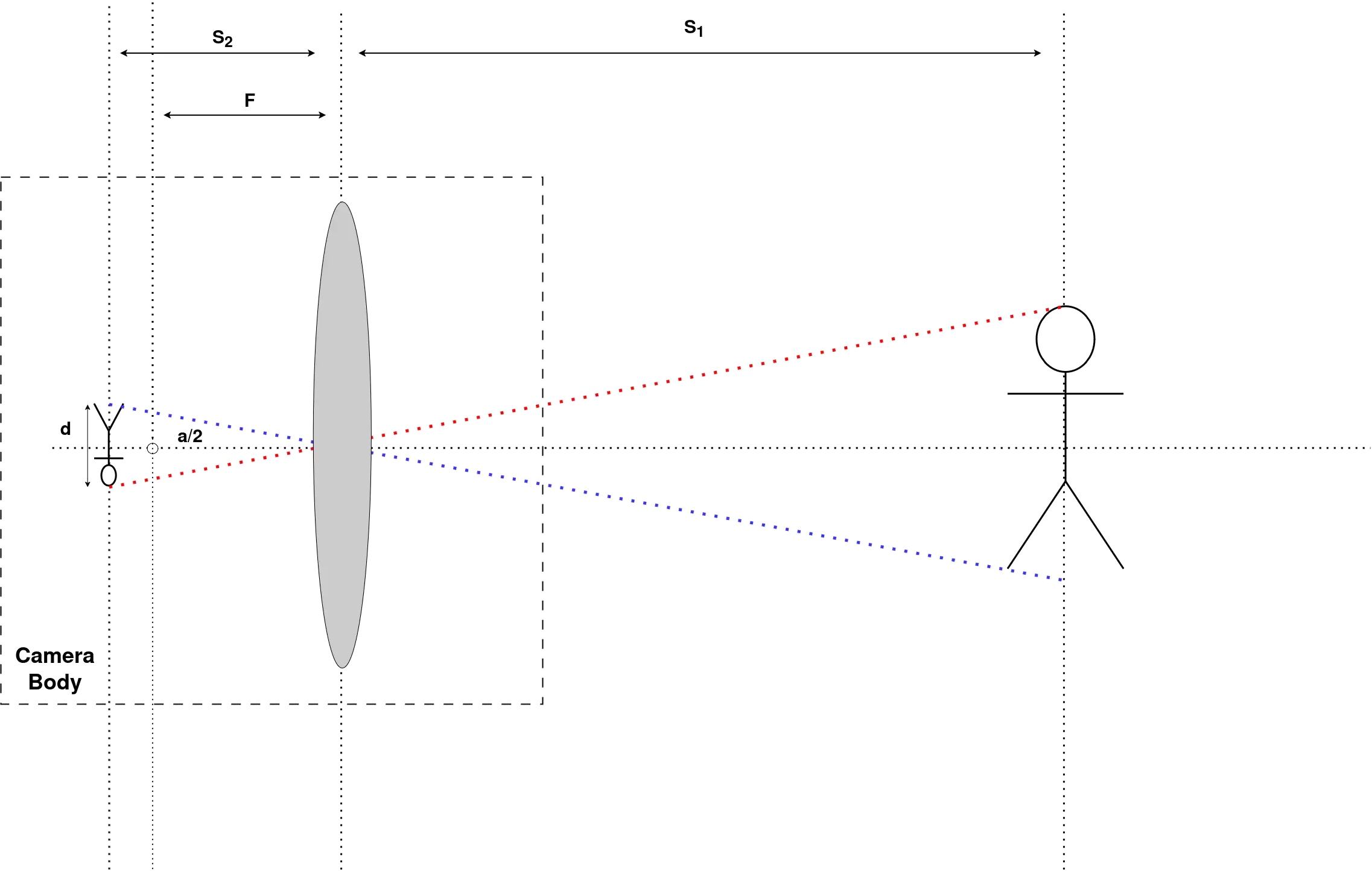
Όπου: \(S_1\) είναι η απόσταση του αντικειμένου από την κάμερα σε \(m\) \(S_2\) η απόσταση του image plane για το pinhole model σε \(m\) \(F\) το focal length σε \(m\), \(d\) το μέγεθος του αντικειμένου στην εικόνα σε \(m\) \(H\) το μέγεθος του αντικειμένου στον πραγματικό κόσμο σε m.

Επίσης, θεωρούμε ότι το αντικείμενο είναι σε focus, συνεπώς \(F=S_2\).

Άρα, με χρήση τριγωνομετρίας και όμοιων τριγώνων, τόσο από την πλευρά του αισθητήρα όσο και του αντικειμένου, καταλήγουμε στην σχέση.

$$ \frac{d}{F} = \frac{H}{S_1} $$

Αν κάνουμε λίγο τα μαθηματικά περισσότερο σε αυτή την σχέση, καταλήγουμε σε μία πολύ ενδιαφέρουσα εκτίμηση.

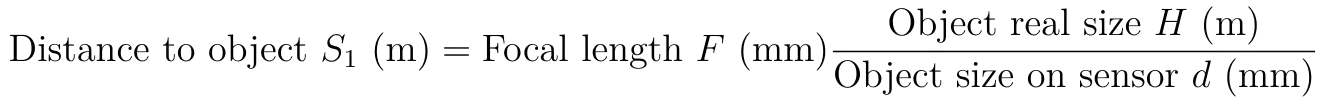
΄Οπου στο μέγεθος του αντικειμένου μπορούμε να χρησιμοποιήσουμε οποιαδήποτε διάσταση επιθυμούμε, όπως το ύψος, το πλάτος ή ακόμα και κάποια διαγώνιο του.

Σε ένα ρεαλιστικό παράδειγμα, θα μετατρέπαμε την προηγούμενη σχέση στην εξής.

Με αυτόν τον τρόπο, αν γνωρίζουμε τις πραγματικές διαστάσεις του αντικειμένου, καθώς και τις παραμέτρους της κάμερας (όπως το focal length, το μέγεθος του sensor και την ανάλυση της εικόνας), μπορούμε απλά, μετρώντας πόσα pixels καταλαμβάνει το αντικείμενο στο image plane, να καθορίσουμε την απόσταση του από την κάμερα.

Αν κάνουμε plot για διάφορες τιμές από pixel - σε ένα use case - αυτή την σχέση, τελικά έχουμε την παρακάτω μη γραμμική εξάρτηση μεταξύ pixels και απόστασης.

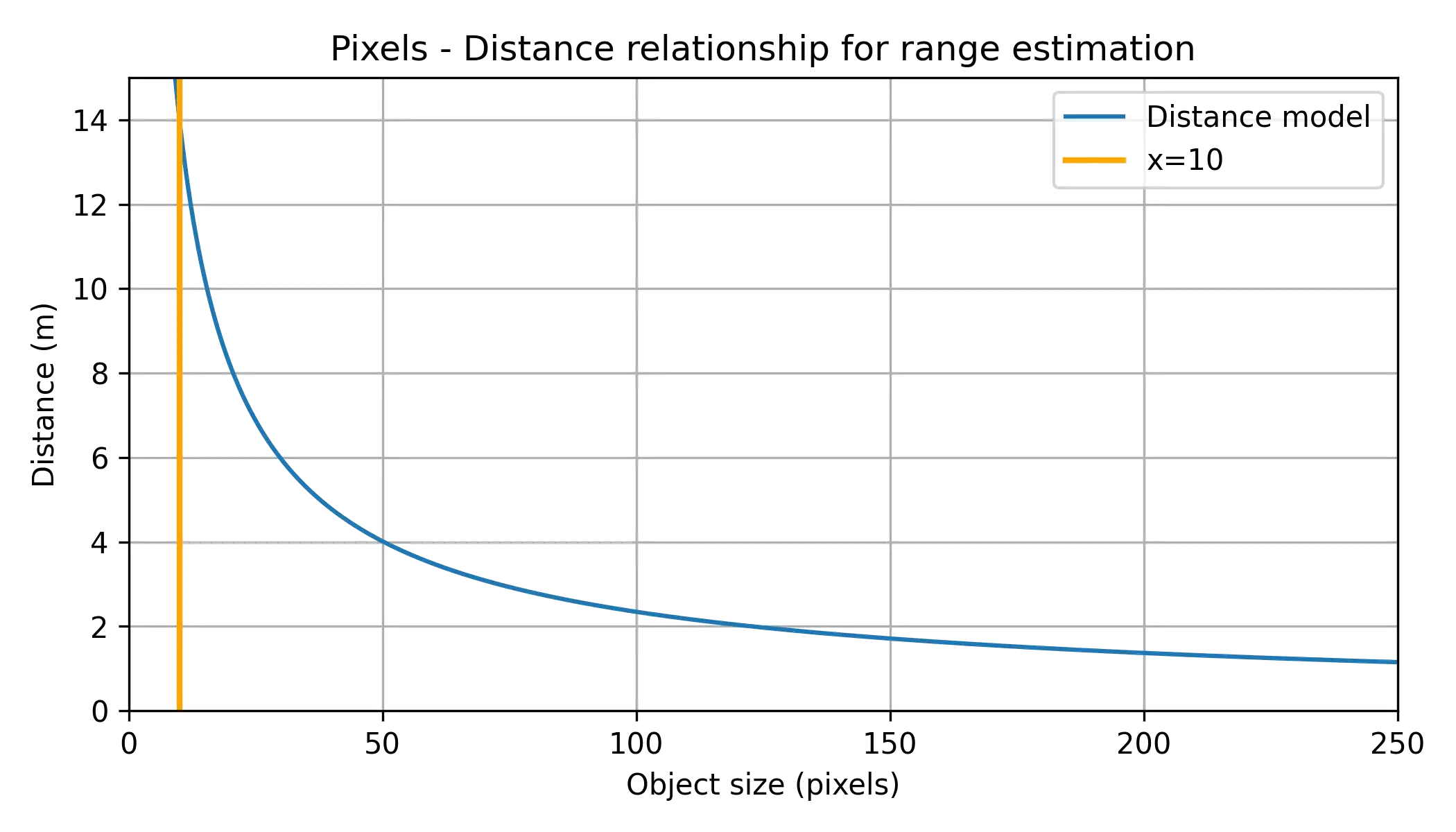
Σε γενικές γραμμές η αναδόμηση της τρίτης διάστασης από single view ακόμα και με ύπαρξη γνωστών αντικειμένων στο scene, μπορεί να καταλήξει να είναι μία εξαιρετικά ασαφής διαδικασία.

Φαντάσου αν το αντικείμενο π.χ. έχει συγκεκρινένη κλίση στην κάμερα και έχει μη συμμετρική γεωμετρία… Τότε τι θα κάνεις;

Για αυτό τον λόγο προσπαθούμε είτε μέσω monocular vision να πάρουμε πολλαπλά views ενός κινούμενου αντικειμένου και να χρησιμοποιήσουμε τεχνικές με όνομα Structure from Motion, είτε από πολλαπλές κάμερες - ονόματι stereo vision - να λάβουμε πολλαπλά views στατικού αντικειμένου για την εκτίμηση τελικά του depth.

🌀 Structure from Motion

Η αρχή λειτουργίας της μεθόδου Structure from Motion είναι η εξαγωγή features από ένα image frame και το tracking τους κατά τη διάρκεια κίνησης της κάμερας.

Με αυτόν τον τρόπο, στο τέλος της διαδικασίας – για το δοθέν sequence of frames – συλλέγεται ένα σύνολο σημείων για κάθε feature \(pf=(xf​,yf​)\) στο image plane της κάμερας (για κάθε frame \(f\)), τα οποία αναπαριστούν το ίδιο σημείο στον φυσικό κόσμο \(P=(x,y,z)\).

Η παρακάτω εικόνα αναπαριστά παράδειγμα αυτής της διαδικασίας.

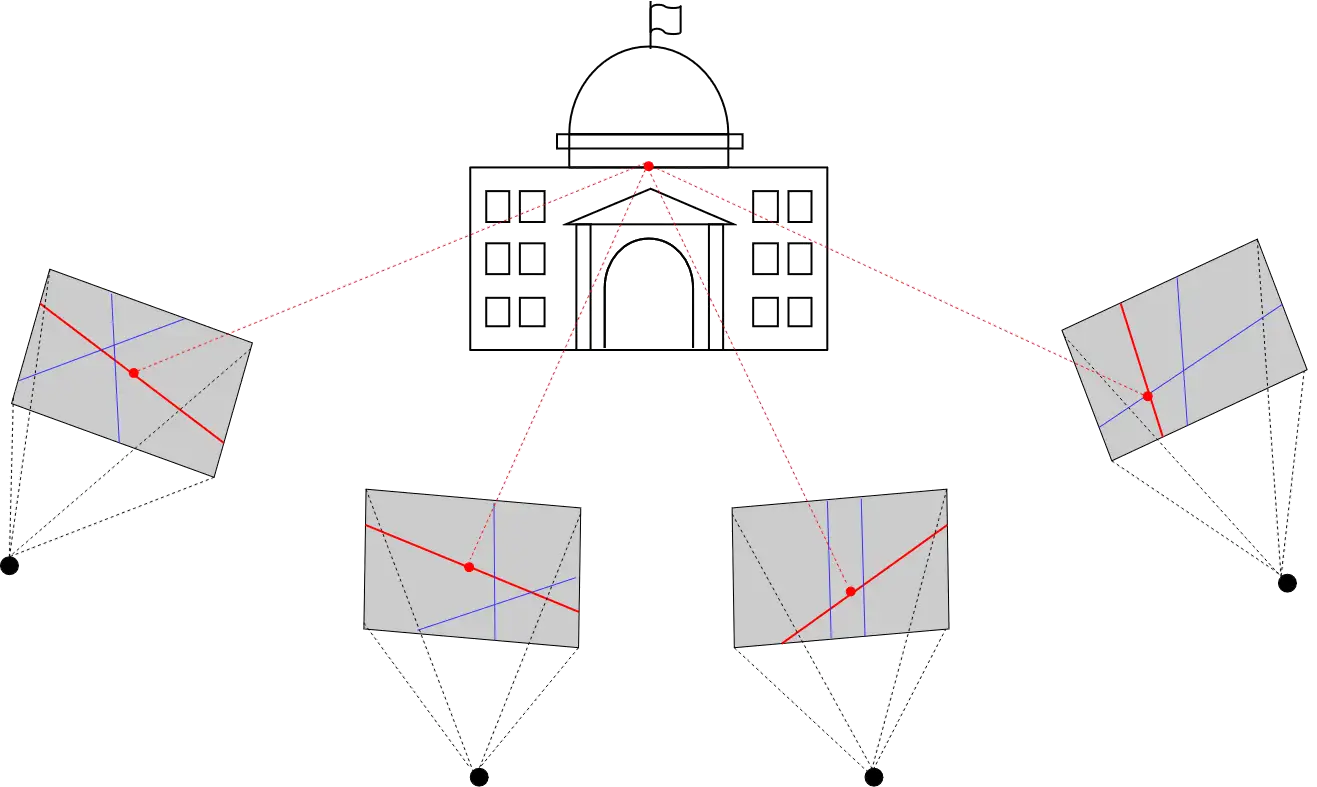
Αφού συλλεχθούν τα παραπάνω δεδομένα, μπορούν να περάσουν από μια πληθώρα αλγορίθμων με ομώνυμο όνομα, μέσω των οποίων μπορεί να προσεγγιστεί η τρισδιάστατη μορφή του αντικειμένου, η κίνηση της κάμερας ή άλλες σημαντικές πληροφορίες.

👀 Stereo Vision

Για τον υπολογισμό του βάθους με χρήση stereo vision, λαμβάνουμε από δύο κάμερες views ενός σκηνικού.

Σε γενίκευση, τα image planes μπορεί να έχουν οποιοδήποτε προσανατολισμό. Μια ειδική περίπτωση – και συχνά πιο χρησιμοποιούμενη – είναι αυτή που παρουσιάζεται παρακάτω, όπου τα image planes είναι παράλληλα.

Προκειμένου να εκτιμηθεί το βάθος με χρήση stereo, γίνονται υπολογισμοί βασισμένοι στο Epipolar Geometry.

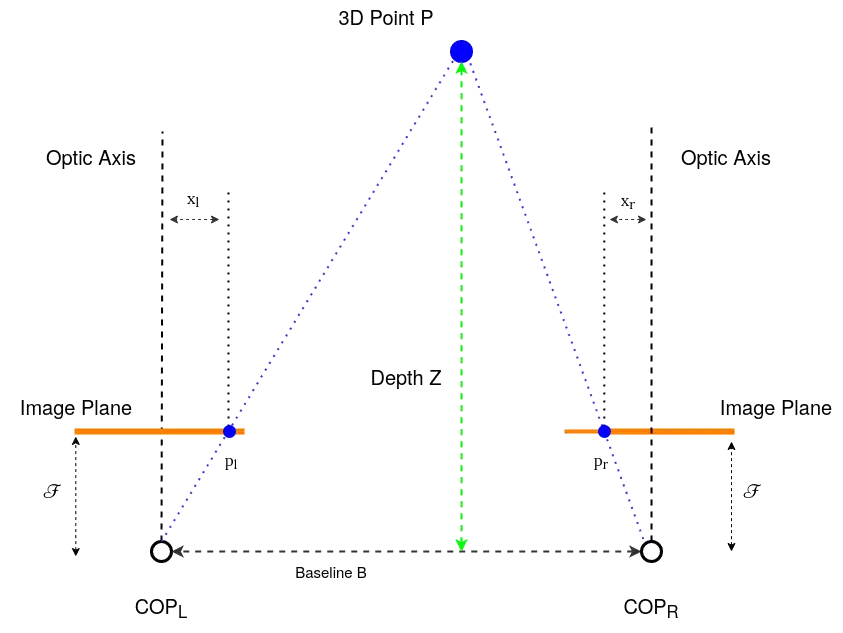
Η Εικόνα αυτή παρουσιάζει τη γεωμετρία στην περίπτωση των parallel optical axes.

Μέσω σχέσεων των όμοιων τριγώνων (pl, P, pr) και (COPL, P, COPR) μπορούμε να δημιουργήσουμε τη σχέση:

$$ \frac{B-x_l+x_r}{Z-F} = \frac{B}{Z} $$

Από την οποία τελικά, μπορούμε να βρούμε ακόμα μία ενδιαφέρουσα εξίσωση για τον υπολογισμό του βάθους ενός σημείου.

$$ Z = F \frac{B}{x_l - x_r} $$

Η ποσότητα xl−xr​ ονομάζεται Disparity, και ουσιαστικά, μετρώντας τη διαφορά της θέσης που εμφανίζεται στο κάθε plane για το σημείο, υπολογίζουμε την απόσταση του σημείου από το baseline των καμερών.

💭 Σύνθεση

Με τις παραπάνω μεθόδους είδαμε, κατά βάση, πώς μπορούμε να ανακατασκευάσουμε την 3η διάσταση που χάνεται από τη δισδιάστατη φύση των frames. Άλλη μία πληροφορία που μπορεί όμως να είναι χρήσιμη είναι και η γωνία που έχει το αντικείμενο από το κέντρο της κάμερας.

Μισό λεπτό…

Θα σε πάω λίγο πίσω… Κάπου στο λύκειο, αν δεν έχεις background με μαθηματικά, ή στα πρώτα έτη της σχολής σε αντίθετη περίπτωση…

Αν ξέρουμε μία απόσταση και γωνίες… τελικά, τι μπορούμε να δημιουργήσουμε;

Διάνυσμα! Πολύ σωστά!

Το διάνυσμα της θέσης του αντικειμένου που μας ενδιαφέρει, με αρχή τους αξόνες της κάμερας!

Ωραίο, δεν ακούγεται;

Τώρα, ποια…

Μάλλον.. μπορούμε να δούμε σε έμπρακτη μορφή πώς είναι εφικτό αυτό που αναφέραμε στην αρχή του άρθρου, δηλαδή τη μεταφορά συντεταγμένων από το image plane, σε πραγματικές συντεταγμένες.

🧭 Εκτίμηση γωνίας

Για την εκτίμηση γωνίας ως προς τον x και y άξονα του image plane σε μία calibrated κάμερα μπορεί να χρησιμοποιηθεί η παρακάτω σχέση η οποία είναι στην πραγματικότητα υλοποίηση απλής μεθόδου των τριών με βάση το Field of View (FOV) μίας κάμερας. Η εικόνα που έχουμε παρακάτω, μάλλον θα βοηθήσει να εξηγηθεί γιατί.

Σε περίπτωση που δεν γνωρίζουμε το FOV, αυτό μπορεί να υπολογιστεί ως προς την συσχέτιση του Angular Field of View (AFOV) με το Focal length της κάμερας, αυτή η εξάρτηση παρουσιάζεται οπτικά σε αυτή εδώ την εικόνα:

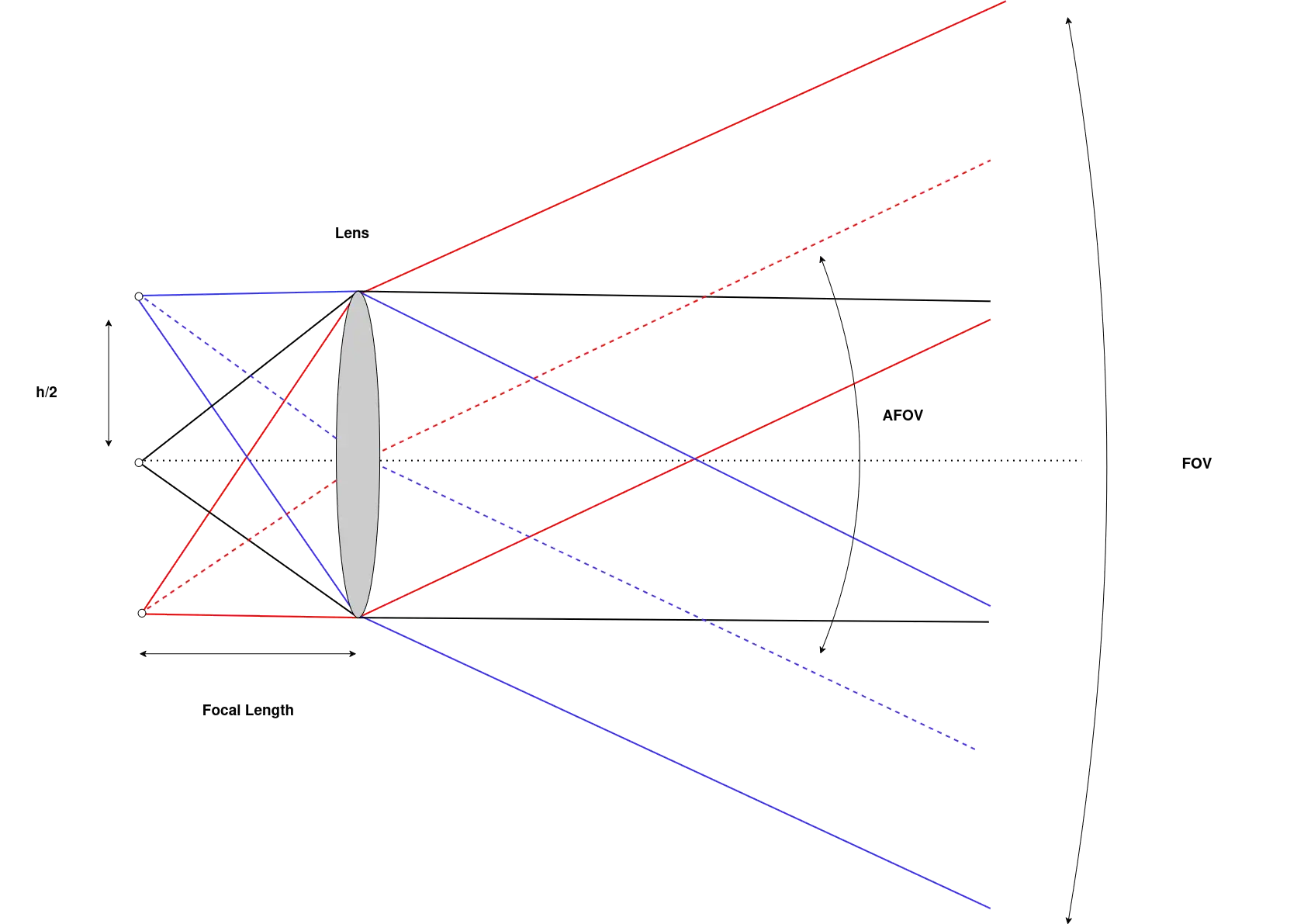
Καλό είναι απλά να θυμόμαστε ότι, όσο αυξάνεται το focal length, μειώνονται τα FOV και AFOV, ενώ όταν μειώνεται το focal length συμβαίνει το αντίθετο.

Ενώ μαθηματικά το ίδιο ακριβώς, αναπαριστάτε με την εξής σχέση.

Μπορούμε να μεταβούμε από το ένα στο άλλο, φυσικά με την εξής μετατροπή:

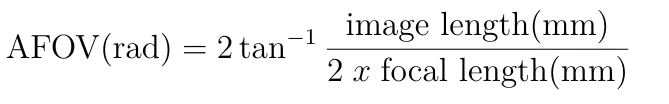
💭 Σύνοψη

Κάπως έτσι, γνωρίζοντας την απόσταση και τις γωνίες, μπορούμε τελικά να εκτιμήσουμε την θέση των αντικειμένων, και ακόμη να χρησιμοποιήσουμε εργαλεία όπως το Matlab για να τα παρουσιάσουμε στον τρισδιάστατο χώρο.

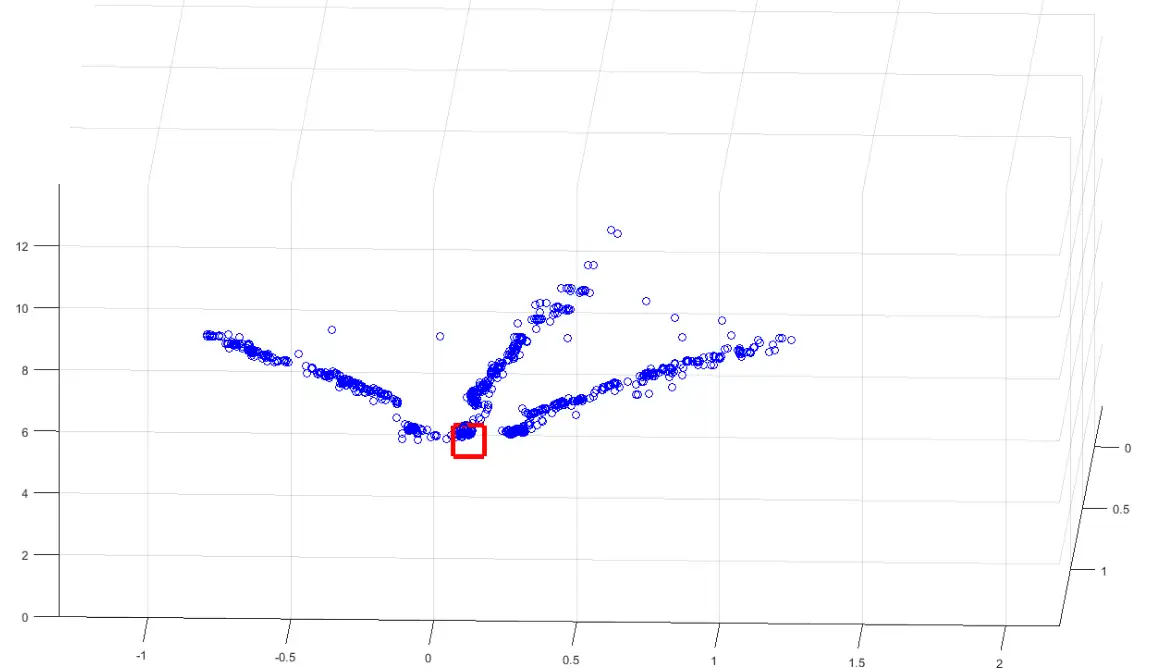
Φυσικά, δεν είναι αυτή η μόνη προσέγγιση που μπορούμε να ακολουθήσουμε…

Το παρόν άρθρο μάλλον δίνει μια επίγευση των μεθοδολογιών, όμως ελπίζουμε να σου αύξησε το ενδιαφέρον για όλες αυτές τις προσεγγίσεις και να σε έκανε να θέλεις να μάθεις περισσότερα για αυτές.

Και πού ξέρεις, ίσως δούμε από εσένα μια υλοποίηση ενός τέτοιου συστήματος στο μέλλον.

🔗 Παραπομπές

[1] Christos Spyridakis, “Design and implementation of a low cost embedded system for localization of drones flying in swarms”, Diploma Work, School of Electrical and Computer Engineering, Technical University of Crete, Chania, Greece, 2022 https://doi.org/10.26233/heallink.tuc.91531 [2] Calculate distance or size of an object in a photo image. [Online]. Available: https://www.scantips.com/lights/subjectdistance.html (visited on 09/2021). [3] A. Rosebrock, Find distance from camera to object/marker using python and opencv, Jul. 2021. [Online]. Available: https://www.pyimagesearch.com/2015/01/19/find-distance-camera-objectmarker-using-python-opencv/ (visited on 09/2021). [4] How do i calculate the distance of an object in a photo? [Online]. Available: https://photo.stackexchange.com/questions/12434/how-do-i-calculate-the-distance-of-an-object-in-a-photo (visited on 09/2021). [5] Epipolar geometry. [Online]. Available: https://en.wikipedia.org/wiki/Epipolar_geometry (visited on 09/2021)