Είναι τελικά η Μουσική η αριθμητική των ήχων;

Έχετε παρατηρήσει ποτέ την αρμονία της μουσικής; Πώς νότες και συγχορδίες μοιάζουν να είναι τέλεια φτιαγμένες και συντονισμένες, σαν κομμάτια παζλ, ώστε να σχηματίζουν όμορφες μελωδίες, και πως ίσως κάποιες άλλες δεν είναι τόσο εύηχες στα αφτιά μας; Ή ακόμα έχετε παρατηρήσει, πως κάποιες μοιάζουν πιο χαρούμενες και κάποιες πιο θλιμμένες;

Ίσως οι παραπάνω προτάσεις σας είναι γνώριμες, ή μπορεί και να έχετε συνδυάσει υποσυνείδητα μια θλιβερή μελωδία με μια συναισθηματικά έντονη ταινία.

Έχετε αναρωτηθεί, όμως, πού αλλού στη φύση συμβαίνει αυτό; Θα σας βοηθήσω λίγο… Στα μαθηματικά! Ναι, δεν σας γελούν τα μάτια σας, διαβάζετε σωστά.

Πώς συνδέονται όμως; Θα μπορούσαμε να χρησιμοποιήσουμε μαθηματικά για να περιγράψουμε την μουσική; Ή θα μπορούσαμε να πούμε πως η μουσική είναι μαθηματικά;

Ήδη από τα αρχαία χρόνια, πολλοί μαθηματικοί και φιλόσοφοι προσπάθησαν να καταλάβουν και να εξηγήσουν αυτή την ομοιότητα και τη σύνδεση μεταξύ αυτών των δύο τεχνών. Ένας από αυτούς ήταν ο Πυθαγόρας.

Ας πάρουμε όμως τα πράγματα από την αρχή. Η δυτική κυρίως μουσική αποτελείται από τις 7 γνωστές σε όλους μας νότες, τοποθετημένες σε μια κλίμακα.

Οι περισσότερες μελωδίες που ξέρουμε είναι φτιαγμένες λόγω αυτού του “σετ” νοτών.

Έχουμε πολλές αναφορές στην αρχαία ιστορία για ένα σύστημα ταξινόμησης νοτών.

Αναφορές που ξεκινούν από τη Μεσοποταμία και φτάνουν ως την Κίνα. Και, όπως οι αναφορές ήρθαν σε εμάς, έφτασαν και στον Πυθαγόρα τον 6ο αιώνα π.Χ., την εποχή που στην αρχαία Ελλάδα κυριαρχούσαν τα έγχορδα μουσικά όργανα.

Ο Πυθαγόρας μελέτησε τη μουσική και ανακάλυψε ότι η αρμονία στις νότες προκύπτει από απλές αριθμητικές αναλογίες. Ειδικότερα, διαπίστωσε ότι εάν τα μήκη δύο χορδών έχουν αναλογίες με μικρούς ακέραιους αριθμούς, οι ήχοι που προκύπτουν είναι εύηχοι.

Μια κλίμακα είναι μια συλλογή από νότες που συνήθως ταξινομούνται με βάση τη συχνότητα ή τον τόνο.

Για παράδειγμα, εάν οι χορδές έχουν μήκη 40 cm και 20 cm, δηλαδή, αναλογία 2:1, προκύπτει μια οκτάβα. Όταν το μήκος της χορδής μειώνεται στο μισό, ο ήχος που παράγεται είναι μια οκτάβα υψηλότερος.

Όταν το μήκος μιας χορδής είναι τα 2/3 του αρχικού μήκους, η αναλογία είναι 3:2 και έτσι προκύπτει μια τέλεια πέμπτη. Και στις δύο περιπτώσεις, θα έχουμε έναν πολύ ευχάριστο ήχο αν παίζουμε τα έγχορδα ταυτόχρονα.

Αν και ο Πυθαγόρας δεν μπορούσε τότε να υπολογίσει την συχνότητα, ήταν εκείνος που κωδικοποίησε μαθηματικά την κλίμακα, ώστε σύγχρονοι να υπολογίσουν πια ότι η συχνότητα f της νότας σε μια κλίμακα οκτάβας δίνεται από τη σχέση: $$ f_n= f_0 * 2^{n/12} $$

Όπου \(f_n\) είναι η συχνότητα της νιοστής νότας, \(f_0\) η συχνότητα της αρχικής νότας και n ο αριθμός των ημιτονίων από την αρχική νότα.

Όταν δύο συχνότητες απέχουν μια οκτάβα, λέμε ότι είναι η ίδια νότα.

Έτσι, κάθε φορά που διπλασιάζουμε ή μειώνουμε στο μισό μια συχνότητα, την ονομάζουμε την ίδια νότα.

Για παράδειγμα, οι συχνότητες των 220Hz, 440Hz, 880Hz αντιστοιχούν στη νότα που ονομάζουμε Λα (A).

Ο Πυθαγόρας, όμως, δεν σταμάτησε εκεί… Παρατήρησε πως, εκτός από την οκτάβα, η επόμενη αρμονική κατάσταση μιας χορδής που δονείται – δηλαδή, το επόμενο «καθαρό» διάστημα, το πιο εύκολο για το αφτί να συντονιστεί – είναι μια πέμπτη.

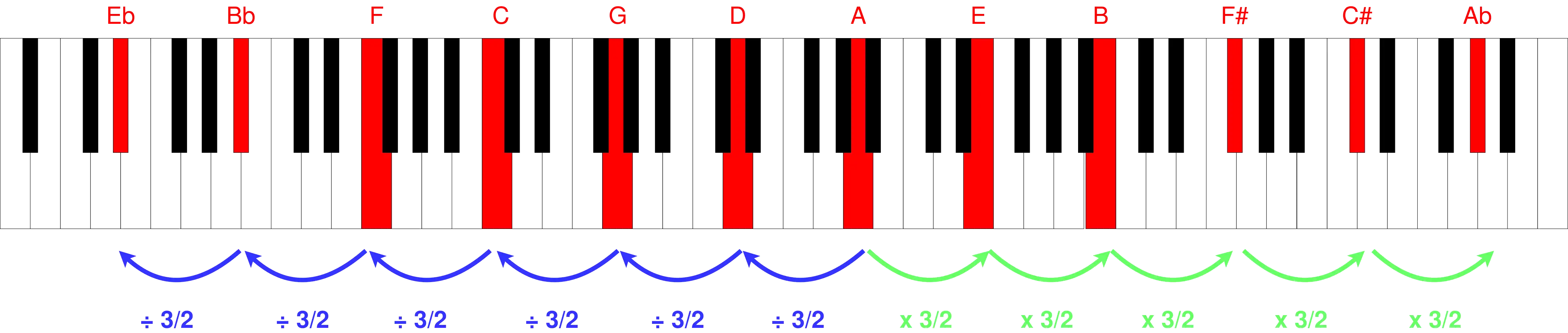
Έτσι, δημιούργησε το Πυθαγόρειο κούρδισμα ή “Pythagorean tuning”, έναν συντονισμό στον οποίο όλα τα κουρδίσματα καθορίζονται επιλέγοντας μια ακολουθία από πέμπτες που βρίσκονται με αναλογία 3:2.

Μια Πυθαγόρεια κλίμακα λοιπόν, είναι οποιαδήποτε κλίμακα που μπορεί να κατασκευαστεί μόνο από τέλειες πέμπτες και οκτάβες.

Αυτή η κλίμακα χρησιμοποιήθηκε ευρέως στην αρχαία ελληνική μουσική και έθεσε τις βάσεις για τη σύγχρονη μουσική θεωρία.

Παρόλο που η Πυθαγόρεια κλίμακα ήταν θεμελιώδης, οι μουσικοί και οι θεωρητικοί της μουσικής διαπίστωσαν ότι μπορούσαν να δημιουργηθούν επιπλέον νότες μέσω διαφορετικών μαθηματικών αναλογιών.

Ένας από τους πρώτους που προχώρησαν πέρα από τον Πυθαγόρα ήταν ο Πτολεμαίος, ο οποίος εισήγαγε την Πτολεμαϊκή κλίμακα χρησιμοποιώντας την αναλογία 5:4 για να ορίσει τη μεγάλη τρίτη, ένα διάστημα που ήταν πιο αρμονικό για τους ακροατές.

Εκτός από τον Πυθαγόρα, ο Ευκλείδης μελέτησε τη μουσική γεωμετρία. Ο αλγόριθμος του Ευκλείδη υπολογίζει τον μέγιστο κοινό διαιρέτη δύο αριθμών, α και β, όπου α>β. Πρώτα διαιρούμε τον α με τον β, παίρνουμε το υπόλοιπο και το ονομάζουμε γ. Μετά διαιρούμε το β με το γ, παίρνουμε το υπόλοιπο αυτής της διαίρεσης και το ονομάζουμε δ. Αν συνεχίσουμε αυτή τη διαδικασία, στο τέλος το υπόλοιπο θα είναι 0. Το τελευταίο μη μηδενικό υπόλοιπο είναι ο μέγιστος κοινός διαιρέτης των αρχικών αριθμών.

Αυτή η ιδιότητα δεν είναι μόνο χρήσιμη για τη δημιουργία ρυθμών στη μουσική, αλλά και για την κατανόηση της σχέσης των μουσικών διαστημάτων. Για παράδειγμα, αν εφαρμόσουμε τον αλγόριθμο του Ευκλείδη στην οκτάβα (αναλογία 2:1) και στην πέμπτη (αναλογία 3:2), μπορούμε να υπολογίσουμε την κατανομή των διαστημάτων σε μια μουσική κλίμακα. Αυτό οδηγεί στη διαίρεση της οκτάβας σε 12 ημιτόνια, όπου κάθε πέμπτη αντιστοιχεί περίπου σε 7 ημιτόνια και κάθε τέταρτη σε 5 ημιτόνια. Έτσι, ο Ευκλείδης, χωρίς να το γνωρίζει, μας έδωσε ένα εργαλείο για την κατανόηση του μουσικού συστήματος όπως το γνωρίζουμε σήμερα.

Ωστόσο, η μουσική θεωρία δεν είναι απόλυτη. Διαφορετικοί πολιτισμοί έχουν υιοθετήσει διαφορετικά μουσικά συστήματα, με αναλογίες και κλίμακες που μπορεί να διαφέρουν από τις δυτικές. Για παράδειγμα, η ινδική μουσική χρησιμοποιεί αναλογίες όπως 7:4 ή 11:8, δημιουργώντας διαφορετικά ηχοχρώματα που μπορεί να ακούγονται «ξένα» σε ένα δυτικό ακροατήριο.

Τελευταίος, για αυτό το άρθρο, αλλά εξίσου σημαντικός, είναι ο αγαπημένος σε όλους μας Fourier. Ενώ ο Ευκλείδης μας βοηθά στην κατανομή των χτυπημάτων και στη διαίρεση των μουσικών διαστημάτων, ο Fourier μας επιτρέπει να αναλύουμε τις ηχητικές κυματομορφές και να τις διασπάμε σε επιμέρους συχνότητες.

Στη μουσική, οι νότες δεν είναι απλοί τόνοι, αλλά αποτελούνται από θεμελιώδεις συχνότητες, όπως μας έδειξε παραπάνω ο Πυθαγόρας. Ο μετασχηματισμός Fourier μας βοηθά να αναλύσουμε αυτές τις συχνότητες και να κατανοήσουμε γιατί ένας ήχος έχει συγκεκριμένο χρώμα. Για παράδειγμα, το ίδιο μουσικό διάστημα μπορεί να έχει διαφορετική ηχητική ποιότητα αν παιχτεί σε ένα πιάνο, ένα βιολί ή ένα σαξόφωνο λόγω των διαφορετικών αρμονικών συνιστωσών.

Και πώς το κάνει αυτό; Μετατρέποντας σύνθετους μουσικούς τόνους από το πεδίο του χρόνου στο πεδίο της συχνότητας. Ο μετασχηματισμός Fourier επιτρέπει την αποδόμηση των ήχων στις συχνότητες που τους συνθέτουν, αποκαλύπτοντας τις μοναδικές αρμονικές δομές που συμβάλλουν στη χαρακτηριστική χροιά διαφορετικών μουσικών οργάνων.

Για να καταλάβουμε πώς λειτουργεί όμως όλο αυτό, αξίζει να ρίξουμε μια ματιά στην μαθηματική εξήγηση πίσω από τις λέξεις.

Ο μετασχηματισμός Fourier μας λέει πως κάθε πολύπλοκο ηχητικό κύμα μπορεί να εκφραστεί ως άθροισμα αρμονικών συνιστωσών:

$$ f(t) =\sum_{n=1}^{\infty}A_n sin(n\omega_0t+\phi_n) $$

όπου \(A_n\)​ είναι το πλάτος κάθε αρμονικής συνιστώσας, \(n\omega_0\) είναι η συχνότητα της n-οστής αρμονικής και \(ϕ_n\)​ είναι η φάση της.

Από αυτήν την εξίσωση καταλαβαίνουμε πως όντως κάθε νότα δεν είναι μια μεμονωμένη οντότητα, αλλά αποτελείται από τη συχνότητα και τις αρμονικές της, και έτσι καθορίζεται το ηχόχρωμα των οργάνων.

Ο συνεχής μετασχηματισμός Fourier ενός σήματος \( f(t) \) χρησιμοποιείται όταν αναλύουμε αναλογικά μουσικά σήματα, όπως για παράδειγμα ο ήχος ενός βιολιού στον αέρα, και ορίζεται ως:

$$ F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt $$ όπου:

- \( f(t) \) είναι η συνάρτηση χρόνου (π.χ., το σήμα ενός ήχου), - \( \omega \) είναι η γωνιακή συχνότητα, \( \omega = 2\pi f \), - \( e^{-i \omega t} \) είναι μια κυματομορφή με συχνότητα \( \omega \), - Το αποτέλεσμα \( F(\omega) \) είναι η ένταση της συχνότητας \( \omega \) που περιέχεται στο σήμα.

Στη σύγχρονη ψηφιακή μουσική και στην επεξεργασία του ήχου, χρησιμοποιούμε την διακριτή εκδοχή του μετασχηματισμού που εφαρμόζεται σε πεπερασμένα σύνολα δεδομένων, όπως για παράδειγμα μια ψηφιακή ηχογράφηση.

Ο διακριτός μετασχηματισμός Fourier (DFT) δίνεται από τη σχέση:

$$ X_k = \sum_{n=0}^{N-1} x_n e^{-i 2\pi k n / N} $$

όπου:

- \( x_n \) είναι τα δείγματα του σήματος, - \( N \) είναι ο συνολικός αριθμός δειγμάτων, - \( k \) είναι ο δείκτης συχνότητας.

Και κάπως έτσι έρχεται η μαγεία: ο Fourier μας δίνει ένα εργαλείο, ένα φακό ας πούμε, για να δούμε τον ήχο με τη γλώσσα των μαθηματικών. Για εμάς πλέον, ένα μουσικό σήμα αναλύεται σε ημιτονοειδή κύματα. Αυτό πρακτικά σημαίνει πως οποιοσδήποτε σύνθετος ήχος μπορεί να αναπαρασταθεί ως άθροισμα απλούστερων ημιτονοειδών κυμάτων, το καθένα με τη δική του συχνότητα, πλάτος και φάση.

Αν μια νότα έχει θεμελιώδη συχνότητα \( f_0 \), οι αρμονικές της βρίσκονται στα πολλαπλάσια αυτής της συχνότητας, όπως \( 2f_0, 3f_0, \dots \)​. Αυτές οι αρμονικές είναι ουσιαστικές για το ηχόχρωμα της νότας, δηλαδή την ποιότητα ή το χρώμα του ήχου που την καθιστά μοναδική.

Με τη μετατροπή του σήματος από τον χρόνο στον χώρο των συχνοτήτων, ο μετασχηματισμός Fourier μας επιτρέπει να δούμε τα διάφορα συστατικά συχνότητας που συνθέτουν τον ήχο, παρέχοντας πολύτιμες πληροφορίες για τη δομή και τα χαρακτηριστικά του.

Από τον Πυθαγόρα, που παρατήρησε τις μαθηματικές σχέσεις στις νότες, τον Ευκλείδη και τη γεωμετρία, αλλά και από πλήθος ακόμη σπουδαίων μαθηματικών στο πέρασμα των αιώνων – που ίσως μπουν σε ένα δεύτερο αφιέρωμα – έως τον Fourier, που ανέλυσε τη δομή τους, υπάρχει μια διαχρονική σύνδεση μεταξύ μαθηματικών και μουσικής.

Κάπως αρκετά σύντομα, λοιπόν, βλέπουμε πως η μουσική και τα μαθηματικά δεν είναι δύο ξεχωριστές έννοιες. Αντ’ αυτού, η μία είναι η γλώσσα της άλλης.

Οι αριθμοί δημιουργούν τις νότες, και οι νότες γίνονται μουσική.

Και όπως δήλωσε και ο Edouard Herriot: «Η μουσική είναι μαθηματικά με ήχο, τα μαθηματικά είναι βουβή μουσική.»

🔗 Παραπομπές

[1] https://www.math.drexel.edu/~dp399/textbooks/mathmusic/pythagorus.html [2] https://en.wikipedia.org/wiki/Pythagorean_tuning [3] https://music.stackexchange.com/questions/115799/ [4] https://plus.maths.org/content/music-and-euclids-algorithm [5] https://scholarship.claremont.edu/cgi/viewcontent.cgi?article=1142&context=jhm [6] https://www.uwlax.edu/globalassets/offices-services/urc/jur-online/pdf/2011/hammond.mth.pdf [7] https://phys.libretexts.org/Bookshelves/Waves_and_Acoustics/Book