Σε προηγούμενο άρθρο γεννήθηκε η απορία για το πώς στο καλό μπορεί να δουλεύει το GPS… Αν έχεις απορία σε ποιο άρθρο έγινε η εισαγωγή, διάβασε αυτό εδώ και θα καταλάβεις 😉.

Ένα από τα σημαντικότερα μέρη ενός συστήματος εντοπισμού θέσης είναι ο υπολογισμός αποστάσεων και γωνιών. Γνωρίζοντας τέτοιου είδους πληροφορίες, μπορούν να χρησιμοποιηθούν έξυπνες μαθηματικές τεχνικές για να βρούμε τις συντεταγμένες της θέσης αντικειμένων στον χώρο και τελικά να βάλουμε στο νέο next-gen phone ένα ultra ακριβές GPS… Πώς μπορεί να γίνει εφικτό, μπορείς να βρεις εδώ.

Σε αυτό το άρθρο θα μιλήσουμε για τεχνικές που αφορούν ακουστικά και ηλεκτρομαγνητικά κύματα. Όταν αναφερόμαστε σε τέτοιες τεχνικές, κατά βάση, εννοούμε μεθοδολογίες που βασίζονται στην ενέργεια, σε αντίθεση με τις οπτικές τεχνικές. Αν σας ενδιαφέρει ο οπτικός τρόπος υπολογισμού της θέσης, με χρήση κάμερας, μπορείτε να διαβάσετε το εξής άρθρο.

📐 A. Εκτίμηση Απόστασης

Το πρώτο που θα μας απασχολήσει είναι, σε ένα σύστημα με 2 κόμβους, n1 και n2, το να μετρήσουμε την απόσταση μεταξύ τους. Αν δεν είναι ξεκάθαρο γιατί αυτό είναι σημαντικό, μην αγχώνεσαι.

Believe in the process. Απλά μείνε μαζί μου, και όσο συνεχίζουμε στο άρθρο ελπίζω ότι θα γίνει ξεκάθαρο.

🛜 Α1. Received Signal Strength

Ξεκινώντας, θα αναφερθούμε σε μια τεχνική που ονομάζεται Received Signal Strength Indicator (RSSI), η οποία χρησιμοποιείται συχνά στα Radio Frequencies (RF) λόγω της απλότητάς της. Εκμεταλλεύεται το γεγονός ότι η λαμβανόμενη ισχύς ενός σήματος εξαρτάται από την απόσταση που βρίσκεται ο δέκτης από τον πομπό.

Συγκεκριμένα, η μείωση της ισχύος ενός σήματος καθώς αυτό διαδίδεται στον χώρο ονομάζεται path loss ή path attenuation.

Στον ελεύθερο χώρο, η λαμβανόμενη ισχύς $P_r(d)$ που ανιχνεύεται από τον δέκτη μπορεί να περιγραφεί από το μοντέλο του Free Space Path Loss (FSPL), το οποίο προκύπτει μέσω της εξίσωσης μετάδοσης του Friis:

$$P_r(d)=\frac{P_t{G}_t{G}_r{\lambda }^2}{(4\pi {)}^2{d}^2}$$

Όπου $P_t$ είναι η ισχύς που στέλνει ο πομπός, $G_t$ είναι το gain της κεραίας του πομπού, $G_r$ το gain της κεραίας του δέκτη, λ το μήκος κύματος του σήματος που μεταδίδουμε και d η απόσταση του πομπού από τον δέκτη. Αν θεωρήσουμε ότι τα $G_t$, $G_r$​ και λ είναι μη μεταβλητές τιμές, επειδή είναι χαρακτηριστικά του hardware που θα χρησιμοποιήσουμε – με $C_f=\frac{G_t{G}_r{\lambda }^2}{(4\pi {)}^2}$ ​– τότε μπορούμε να καταλήξουμε στην παρακάτω σχέση:

$$P_r(d)=C_f\frac{P_t}{d^2}$$

Τι μας λέει τώρα αυτό; Ωραία τα μαθηματικά, αλλά δεν γίνεται να έχουμε τελειώσει και Πανεπιστήμιο για να τα καταλάβουμε όλα…

Πρακτικά… Κράτα ένα πράγμα! Αυτό που μπορούμε να δούμε από την παραπάνω σχέση είναι ότι, ιδανικά, στον ελεύθερο χώρο, σε μετάδοση Line of Sight (LoS) – δηλαδή, όταν ο πομπός βλέπει τον δέκτη χωρίς να υπάρχουν ενδιάμεσα εμπόδια, η ισχύς του σήματος που λαμβάνει ο δέκτης εξαρτάται από το αντίστροφο του τετραγώνου της απόστασης μεταξύ των δύο nodes.

Η τελευταία σχέση που μόλις δώσαμε συχνά αναφέρεται σε watt, όμως, όταν αναφερόμαστε στην ισχύ μετάδοσης, πολύ συχνά μας βολεύει να την εκφράζουμε σε dBm. Ο τρόπος για να μετατρέψουμε watt σε dBm και αντίστροφα μπορεί να γίνει με τις παρακάτω σχέσεις.

$$P[dBm]=10\cdot lo{g}_{10}\left(\frac{P[mW]}{1[mW]}\right)$$ $$P[mW]={10}^{\frac{(P[dBm])}{10}}$$

Ωραία… Και τώρα που έχουμε πει όλα αυτά, ας δούμε λίγο οπτικά τι σημαίνει η πρόταση: “η ισχύς του σήματος που λαμβάνει ο δέκτης εξαρτάται από το αντίστροφο του τετραγώνου της απόστασης μεταξύ των δύο nodes”. Ας αναπαραστήσουμε την σχέση που αναφέραμε νωρίτερα, η οποία συνδέει την απόσταση του πομπού από τον δέκτη με τη λαμβανόμενη ισχύ σε dBm.

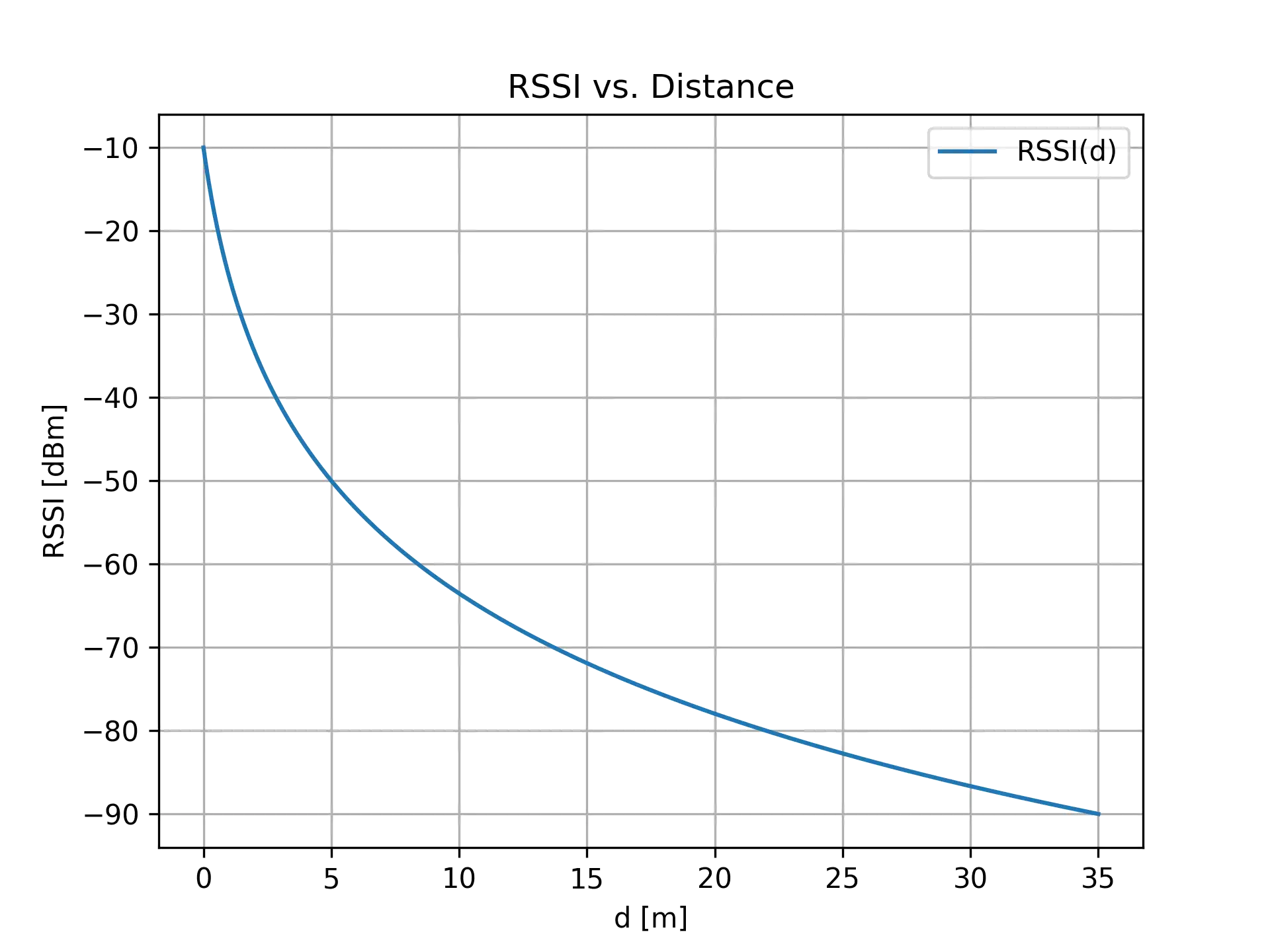
Αν λοιπόν, μετράμε την ισχύ με την οποία λαμβάνουμε ένα σήμα, μπορούμε να είμαστε σε θέση να υπολογίσουμε την απόσταση που βρίσκεται ο πομπός από εμάς. Αυτή η μέθοδος παρόλο που είναι αρκετά δημοφιλής και οικονομική για τον υπολογισμό της απόστασης - λόγω του ότι δεν απαιτεί επιπλέον αισθητήρες - σε πραγματικές συνθήκες αντιμετωπίζει αρκετά προβλήματα, καθώς οι μετρήσεις μπορούν να επηρεαστούν από θόρυβο, ανακλάσεις του σήματος, διαθλάσεις, δυναμικά περιβάλλοντα ή εμπόδια σε αυτά, Non-Line of Sight (NLoS) μετάδοση, ή ακόμα και errors στο hardware. Σε ένα βαθμό μπορεί να βελτιωθεί η απόδοση με στατικό ή δυναμικό calibration του συστήματος, όμως μέχρι τώρα δεν χρησιμοποιείται για εκτίμηση απόστασης σε εφαρμογές όπου nodes έχουν μεγάλη απόσταση μεταξύ τους ή μας ενδιαφέρει να έχουμε μεγάλη ακρίβεια προσέγγισης της απόστασης

🕐 Α2. Propagation Time

Σε αυτήν την κατηγορία εκτίμησης απόστασης μεταξύ nodes - η οποία βασίζεται σε χρονικές μετρήσεις της διάδοσης του σήματος, Time of Flight (ToF) - κατά κύριο λόγο χρησιμοποιούνται δύο βασικές τεχνικές, η Time of Arrival (ToA) και η Time Difference of Arrival (TDoA).

Α2.1 Time of Arrival

Aπό την κινηματική γνωρίζουμε την παρακάτω σχέση:

$$V=\frac{\mathrm{d}s}{\mathrm{d}t}$$

Η οποία συσχετίζει την ταχύτητα κίνησης ενός σώματος V ως το πηλίκο της μεταβολής της θέσης ds - που έκανε το σώμα - προς τον χρόνο dt που χρειάστηκε για να πραγματοποιηθεί η μεταβολή. Αξιοποιώντας αυτή την σχέση ως αρχή, μπορούμε να καταλήξουμε στην επόμενη σχέση ώστε να εκτιμήσουμε την απόσταση d που βρίσκονται δύο nodes μεταξύ τους, αν ένα κύμα κινείται με ταχύτητα s και χρειάστηκε χρόνο t για να μεταδοθεί από το ένα node στο άλλο.

$$d=s(t_b-t_a)$$

Στο (a) απεικονίζεται σχηματικά αυτή η ιδέα, όπου $t=t_b-t_a$ με $t_b$ η χρονική στιγμή που φτάνει το κύμα στο receiver και $t_a$ η χρονική στιγμή η οποία ξεκινάει από τον transmitter. Σε περίπτωση που μιλάμε για RF κύματα και μετάδοση στο κενό, η ταχύτητα μετάδοσης του κύματος είναι ίση με την ταχύτητα μετάδοσης του φωτός $c_o$, το οποίο σε $0.1\mu s$ διανύει περίπου $30m$.

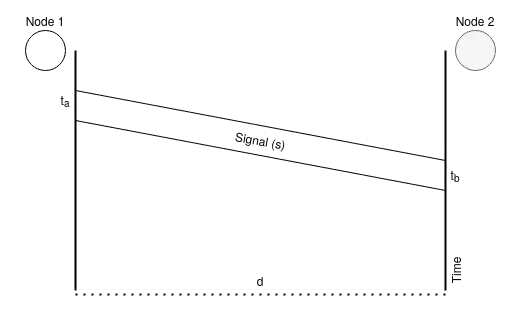
Κατάλαβες τι γίνεται εδώ…; Μετρώντας τον χρόνο που χρειάζεται ένα σήμα για να μεταδοθεί μεταξύ δύο σημείων, μπορούμε τελικά να υπολογίσουμε την απόσταση τους.

Με βάση αυτό, μπορούμε εύκολα να καταλάβουμε ότι για να έχουμε ακριβή αποτελέσματα είναι αρκετά σημαντικό τα clocks των δύο nodes να είναι απόλυτα συγχρονισμένα για να μην έχουμε error απόκλισης, πράγμα που απαιτεί να κάνουμε το συνολικό σύστημα αρκετά πιο πολύπλοκο σχεδιαστικά ώστε η απόκλιση μας να είναι σε ανεκτά σημεία για την εφαρμογή.

Μπορούμε να το παρακάμψουμε αυτό, με το να γίνει η μέτρηση σε Round-Trip Time (RTT), βλ. (b).

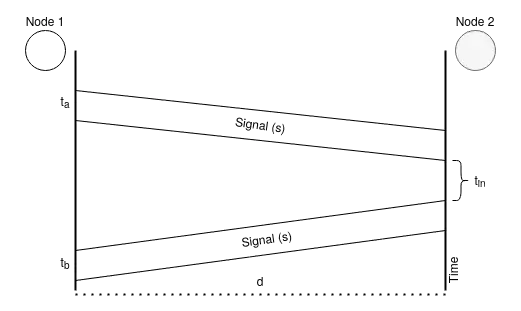
Σε αυτήν την περίπτωση το ένα node στέλνει ένα σήμα, και μόλις το λάβει ένα γειτονικό node, απαντάει πίσω στο πρώτο. Με αυτόν τον τρόπο η μέτρηση του χρόνου εκκίνησης $t_a$ και άφιξης $t_b$ του σήματος γίνονται στο ίδιο node - άρα δεν χρειάζεται συγχρονισμός, και η πραγματική απόσταση είναι η μισή από αυτή που θα υπολογιστεί. Ο κύριος παράγοντας σφάλματος σε αυτή την μέθοδο, είναι ο υπολογισμός του χρόνου που χρειάστηκε το δεύτερο node για να διαχειριστεί το σήμα που έλαβε και να απαντήσει. Αυτό το internal delay $t_{in}$ μπορεί να είναι είτε γνωστό από ένα a priori calibration, είτε μπορεί να μετριέται και να στέλνεται μαζί με το σήμα απάντησης - ώστε να αφαιρείται από τον χρόνο μετάδοσης του κύματος.

Με αυτά τα δεδομένα, η παρακάτω σχέση μπορεί να περιγράφει τον τρόπο υπολογισμού της απόστασης d μεταξύ των δύο nodes ακολουθώντας αυτή την μεθοδολογία:

$$d=\frac{s(t_b-t_a-t_{in})}{2}$$

Α2.2 Time Difference of Arrival

Όσον αφορά την τεχνική TDoA, και σε αυτήν την περίπτωση υπάρχουν δύο παραλλαγές της, όπου και οι δύο είναι βασισμένες στην αρχή το ότι δεν μας ενδιαφέρει η χρονική στιγμή που ξεκίνησε η αποστολή ενός σήματος, αλλά μόνο η χρονική στιγμή που το λάβαμε.

Η πρώτη περίπτωση σχετίζεται με single signal και multiple receivers και παρουσιάζεται στο (c).

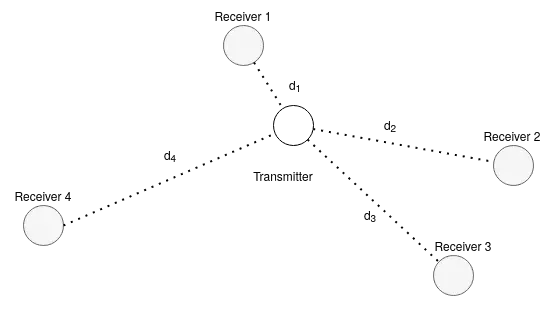
Χρησιμοποιείται συνήθως στα cellular networks και απαιτεί την ύπαρξη τουλάχιστον 4 beacons για την απόκτηση πληροφοριών τοποθεσίας ενός free node στον τρισδιάστατο χώρο. Υπολογίζει τη χρονική διαφορά με την οποία έφτασε το σήμα που έστειλε το free node σε κάθε beacon για την εκτίμηση της θέσης του free node από το καθένα από αυτά. Σημαντικό σε αυτήν την περίπτωση είναι, και πάλι, να είναι απόλυτα συγχρονισμένοι οι receivers, αλλά επειδή συνήθως σε τέτοιες εφαρμογές πρόκειται για επίγειες συσκευές με ενσύρματη διασύνδεση, αυτό είναι πιο εύκολο. Βασίζεται στις ιδιότητες των υπερβολικών καμπυλών και στο γεγονός ότι, με δεδομένη μια συγκεκριμένη χρονική διαφορά του σήματος, το free node θα πρέπει να βρίσκεται κάπου πάνω σε μια υπερβολική καμπύλη.

Παρακάτω παρατίθενται παραδείγματα για διαφορετικά Δt (χρονική διαφορά με την οποία λαμβάνουμε σήματα).

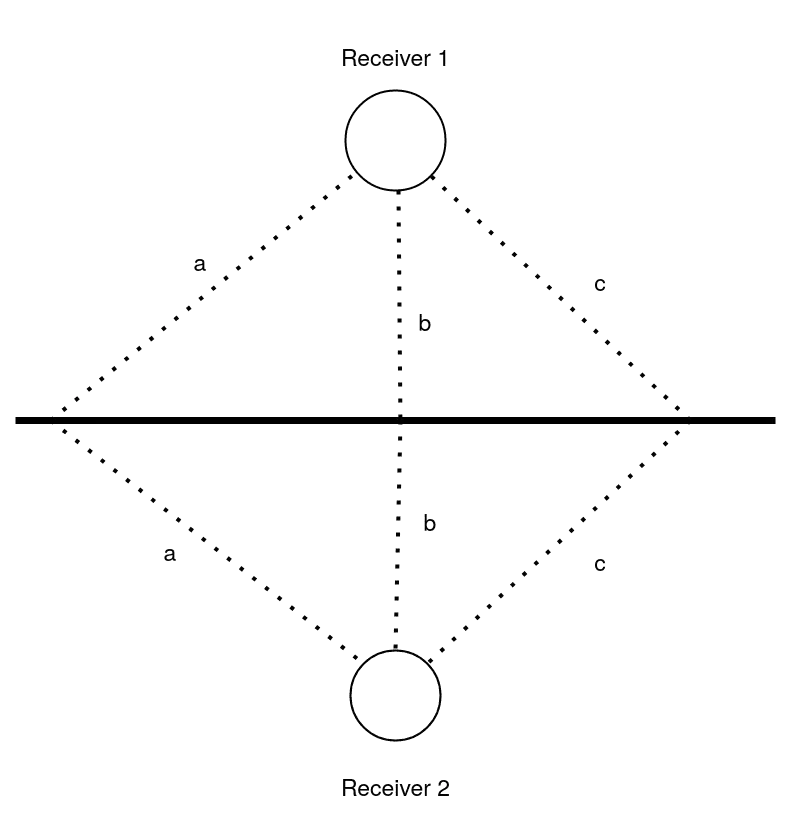
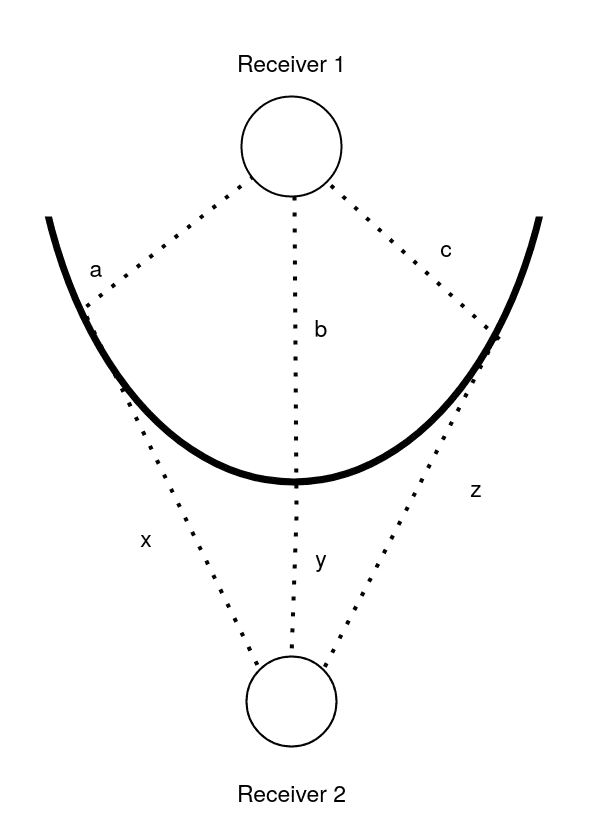
$$\mathrm{\Delta }t=x-a$$ $$\mathrm{\Delta }t=y-b$$ $$\mathrm{\Delta }t=z-c$$

Η δεύτερη εκδοχή της χρήσης TDoA - η οποία είναι πιο συχνή στα Wireless Sensor Networks (WSN), χρησιμοποιεί multiple signals με single receiver.

Η συγκεκριμένη μέθοδος είναι διαισθητικά παρόμοια, με αυτό που θα κάναμε για να εκτιμήσουμε την απόσταση μίας αστραπής από εμάς, μετρώντας το χρονικό διάστημα μέχρι να ακούσουμε την βροντή.

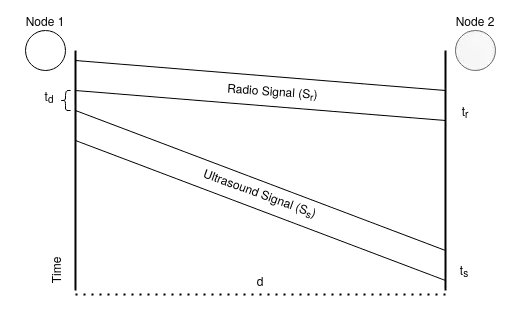
Η αρχή λειτουργίας είναι ότι ο transmitter θα στείλει πολλαπλά, διαφορετικού είδους, σήματα και ο δέκτης θα μετρήσει τη χρονική διαφορά που τα έλαβε. Ως παράδειγμα, μπορεί το ένα σήμα να είναι σε RF και να κινείται με ταχύτητα $s_r=c_o$​ και το άλλο, ηχητικό, με ταχύτητα $s_s\approx 343m/s$ (για μετάδοση σε ξηρό αέρα υπό θερμοκρασία $20°C$). Αν $t_r$ είναι η χρονική στιγμή που λαμβάνει το RF σήμα, $t_s$ η χρονική στιγμή που λαμβάνει το ηχητικό και $t_d$ το delay που μεσολάβησε από την αποστολή του ενός στο άλλο, τότε μπορούμε να υπολογίσουμε την απόσταση μεταξύ των κόμβων από την εξίσωση:

$$d=(s_r-s_s)(t_s-t_r-t_d)$$

Θετικό σε αυτήν τη μέθοδο είναι ότι το error μπορεί να είναι της τάξης των μερικών εκατοστών, όμως αρχικά απαιτεί επιπλέον εξοπλισμό στο node – ώστε να μπορεί να στείλει και να λάβει πολλαπλά είδη σήματος – πράγμα που μπορεί να το καταστήσει αντιοικονομικό ή αρκετά μεγαλύτερο σε διαστάσεις από το επιθυμητό το ολικό σύστημα. Επιπλέον – και μάλιστα σημαντικότερο, η απόσταση που μπορεί να χρησιμοποιηθεί επηρεάζεται σε μεγάλο βαθμό από τα χαρακτηριστικά του δεύτερου σήματος. Ως παράδειγμα, τα ηχητικά σήματα δεν μπορούν να μεταφερθούν σε μεγάλες αποστάσεις, ενώ η ταχύτητά τους μπορεί να επηρεαστεί σημαντικά από περιβαλλοντολογικούς παράγοντες.

🧭 B. Εκτίμηση Γωνίας

Άλλη μία χρήσιμη μέτρηση η οποία μας ενδιαφέρει, είναι η εκτίμηση της γωνίας από την οποία λαμβάνουμε το σήμα ενός γειτονικού node σε σχέση με έναν άξονας αναφοράς. Ο άξονας αυτός μπορεί να είναι είτε κοινώς για όλα τα nodes (π.χ. ως προς το βόρειο γεωγραφικό πόλο), είτε μπορεί να είναι για το κάθε node ξεχωριστός, ως παράδειγμα με βάση τον προσανατολισμό του ίδιου του node ή με βάση την γωνία λήψης ενός επιπλέον σήματος. Την πληροφορία αυτή την βρίσκουμε στην βιβλιογραφία να ονομάζεται Angle of Arrival (AoA) ή Direction of Arrival (DoA).

$$s(t)=A\sin (2\pi ft+\varphi )$$

Γνωρίζουμε ότι ένα σήμα καθορίζεται πλήρως από τρεις παραμέτρους, το πλάτος του A, την συχνότητα του f καθώς επίσης και από την φάση του $\varphi$. Για τον υπολογισμό της γωνίας AoA μπορούν να χρησιμοποιηθούν τεχνικές με γνώμονα τα παραπάνω.

Β1. Amplitude response

Ο όρος Beamforming χρησιμοποιείται για να περιγράψει το pattern της ευαισθησίας του σήματος που στέλνει/λαμβάνει μία directional antenna. Το pattern αυτού του τύπου κεραίας, παρουσιάζεται σε αυτή την εικόνα.

Μπορούμε λοιπόν να χρησιμοποιήσουμε αυτό το χαρακτηριστικό για τον υπολογισμό της AoA.

Εάν χρησιμοποιούμε directional antenna στον receiver και μπορούμε είτε με μηχανικό είτε με ηλεκτρονικό τρόπο να στρέψουμε την κεραία σε διάφορες κατευθύνσεις, τότε μπορούμε μετρώντας το πλάτος του σήματος που λαμβάνουμε, να εκτιμήσουμε και την κατεύθυνση του - όπου ιδανικά βρίσκεται εκεί από όπου έχουμε την μέγιστη τιμή του amplitude του κύματος.

Σημαντικές παράμετροι για την εκτίμηση της γωνίας σε αυτήν την περίπτωση, είναι επίσης η ευαισθησία του δέκτη καθώς και το width του beam της.

Λανθασμένη εκτίμηση μπορεί να προκύψει, αν για κάποιο λόγο το πλάτος του σήματος που λαμβάνουμε δεν είναι σταθερό.

Σε αυτή την περίπτωση, μία λύση είναι να χρησιμοποιήσουμε μία δεύτερη - μη κινούμενη - omnidirectional κεραία και να κανονικοποιήσουμε τις μετρήσεις της directional με βάση τις μετρήσεις της δεύτερης.

Β2. Phase response

Άλλος τρόπος υπολογισμού του AoA είναι με την αξιοποίηση της πληροφορία για την φάση που έχουμε για ένα σήμα. Σε αυτήν την περίπτωση χρειαζόμαστε ή κεραίες αρκετά μεγαλύτερες από το μήκος κύματος του σήματος που στέλνουμε, ή antenna arrays.

Για τα κύματα γνωρίζουμε (μην ρωτάς πώς το γνωρίζουμε 😝 – δεν έχει σημασία να τα αναλύσουμε όλα, αλλά να δημιουργήσουμε την περιέργεια για περαιτέρω αναζήτηση) ότι η διαφορά φάσης $\mathrm{\Delta }\varphi$ δύο σημείων που απέχουν μεταξύ τους $\mathrm{\Delta }\chi$ μπορεί να υπολογιστεί από την αυτή την σχέση:

$$\mathrm{\Delta }\varphi =2\pi \frac{\mathrm{\Delta }\chi }{\lambda }=2\pi \frac{\mathrm{\Delta }t}{T}$$

Συνεπώς, αν σχεδιάσουμε ένα antenna array, όπου η κάθε κεραία απέχει από την γειτονική της σε συγκεκριμένη απόσταση d και μετρώντας το phase difference του σήματος που λαμβάνουμε μεταξύ τους, τότε μπορούμε να υπολογίσουμε την γωνία πρόσληψης της ακτινοβολίας μέσω της σχέσης:

$$\varphi =\frac{2\pi }{\lambda }d\sin (\theta )\Rightarrow$$ $$\theta ={\sin }^{-1}\left(\frac{\lambda \varphi }{2\pi d}\right)(1)$$

Παράδειγμα αυτού βρίσκεται παρακάτω, όπου χρησιμοποιούμε omnidirectional κεραίες και o υπολογισμός της διαφοράς φάσης μπορεί να γίνει μέσω μετρήσεων TDoA.

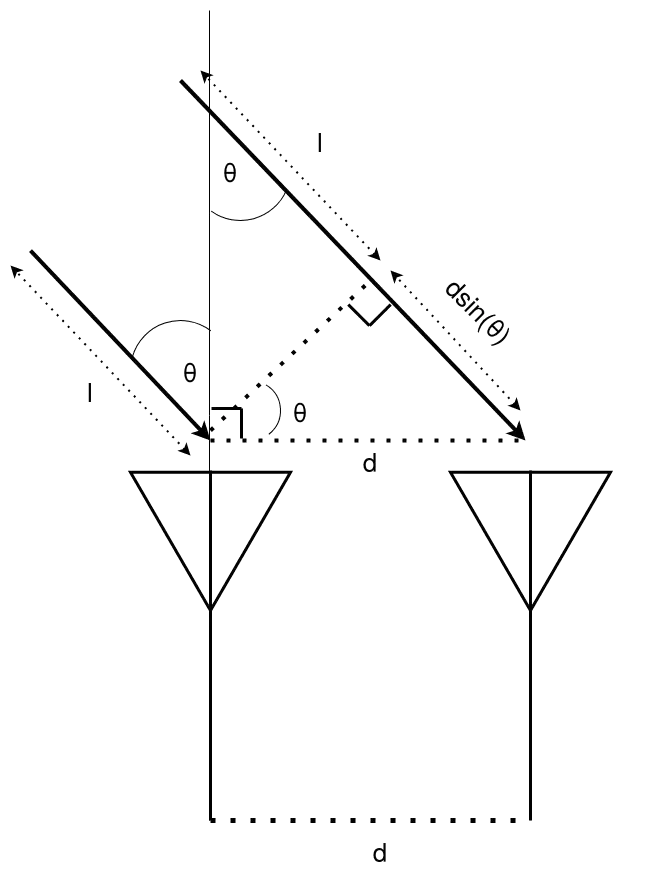
Δεν υπάρχουν όμως μόνο τα linear antenna arrays, μπορούμε να τα σχεδιάσουμε σε διάφορες διατάξεις, παράδειγμα μίας εξ’ αυτών βρίσκετα σε αυτή την εικόνα:

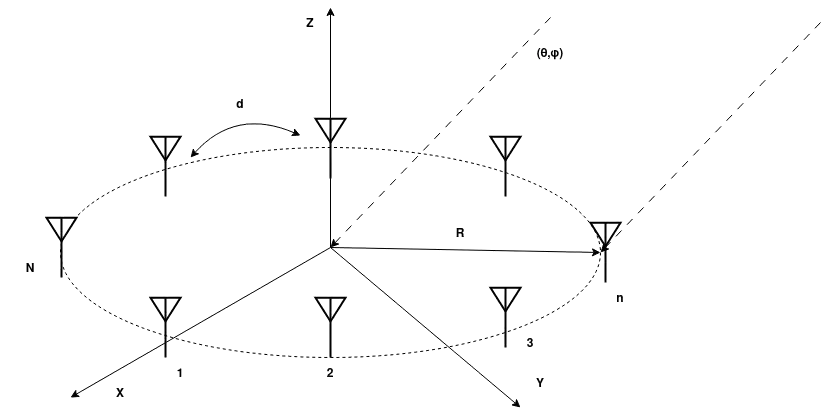
Η μέθοδος με την αξιοποίηση της σχέσης (1) λειτουργεί αρκετά καλά όταν έχουμε υψηλό Signal to Noise Ratio (SNR), αλλά μπορεί να έχει λανθασμένα αποτελέσματα όταν έχουμε διασυμβολικές παρεμβολές ή multipath signals.

Επειδή στην πράξη εμφανίζονται και τα δύο, υπάρχει αρκετά μεγάλο επιστημονικό ενδιαφέρον να αντιμετωπιστεί αυτός ο περιορισμός. Αρκετές τεχνικές έχουν προταθεί οι οποίες στρέφονται γύρω από την λογική του Maximum Likelihood (ML) για τον υπολογισμό τελικά της γωνίας.

💭 Σύνοψη

Στο συγκεκριμένο άρθρο πήραμε μια πρώτη γεύση διάφορων τεχνικών που υπάρχουν ήδη, οι οποίες χρησιμοποιούν την ενέργεια για τον υπολογισμό απόστασης/γωνίας μεταξύ δύο σημείων.

Το ερώτημα, όμως, παραμένει…

Πώς μπορούμε να υπολογίσουμε την θέση αντικειμένων στο χώρο;

Έστω ότι γνωρίζουμε διάφορες αποστάσεις και γωνίες, μπορούν τέτοιες πληροφορίες να συνδυαστούν για να επιτύχουμε εκτίμηση της θέσης μας στον τρισδιάστατο χώρο;

Φυσικά και μπορούμε!

Σε αυτό το άρθρο βλέπουμε πώς είναι εφικτό να γίνει αυτό.

🔗 Παραπομπές

[1] Christos Spyridakis, “Design and implementation of a low cost embedded system for localization of drones flying in swarms”, Diploma Work, School of Electrical and Computer Engineering, Technical University of Crete, Chania, Greece, 2022 https://doi.org/10.26233/heallink.tuc.91531 [2] R. Peng and M. L. Sichitiu, “Angle of arrival localization for wireless sensor networks,” in 2006 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks, vol. 1, 2006, pp. 374–382. doi: 10.1109/SAHCN.2006.288442. [3] B. Yamamoto, A. Wong, P. J. Agcanas, K. Jones, D. Gaspar, R. Andrade, and A. Z. Trimble, “Received signal strength indication (rssi) of 2.4 ghz and 5 ghz wireless local area network systems projected overland and sea for near-shore maritime robot operations,” Journal of Marine Science and Engineering, vol. 7, no. 9, p. 290, Aug. 2019, issn: 2077-1312. doi: 10.3390/jmse7090290. [Online]. Available: http://dx.doi.org/10.3390/jmse7090290. [4] K. Benkic, M. Malajner, P. Planinsic, and Z. Cucej, “Using rssi value for distance estimation in wireless sensor networks based on zigbee,” pp. 303–306, 2008. doi: 10.1109/IWSSIP.2008.4604427. [5] Path loss. [Online]. Available: https://en.wikipedia.org/wiki/Pathloss (visited on 12/2020). [6] Free-space path loss. [Online]. Available: https://en.wikipedia.org/wiki/Free-space_path_loss (visited on 12/2020). [7] Friis transmission equation. [Online]. Available: https://en.wikipedia.org/wiki/Friis_transmission_equation (visited on 12/2020). [8] Dbm. [Online]. Available: https://en.wikipedia.org/wiki/DBm (visited on 12/2020). [9] Kinematics. [Online]. Available: https://en.wikipedia.org/wiki/Kinematics (visited on 12/2020). [10] An introduction to direction findin, Feb. 2020. [Online]. Available: https://www.youtube.com/watch?v=N8rZIAHxAH4 (visited on 12/2020).