Αλγόριθμοι σχετικά με τον υπολογισμό θέσης αντικειμένων

Όλο απορίες είμαστε…

Βλέπεις, σε προηγούμενα άρθρα ξεκινήσαμε να βλέπουμε θέματα σχετικά με το GPS και τον εντοπισμό της θέσης αντικειμένων. Είδαμε ακόμα και πώς είναι εφικτό να υπολογίσουμε αποστάσεις και γωνίες μεταξύ δύο συσκευών, που είναι πρακτικά το πρώτο βήμα για να υπολογίσουμε πού βρίσκεται ένα αντικείμενο στον χώρο.

Μετά πηδήξαμε σε ένα γειτονικό θέμα, όπου χρησιμοποιούμε αυτές τις αποστάσεις και τις γωνίες που υπολογίσαμε για να μελετήσουμε, μέσω αλγορίθμων, αυτό που είχαμε εξαρχής σαν στόχο: τις συντεταγμένες του στον χώρο.

Σε ένα πραγματικό σύστημα όμως πρέπει να συνυπολογιστούν και άλλοι παράγοντες πέρα από - απλά - τον υπολογισμό απόστασης/γωνίας για να καταλήξουμε να αποκτήσουμε location information.

Για αυτό το λόγο, στο παρόν άρθρο παρουσιάζονται επιπλέον πτυχές του συστήματος που πρέπει να λάβουμε υπόψιν, καθώς και αναφορά αλγορίθμων από την υπάρχουσα βιβλιογραφία, με τους οποίους μπορούμε να καλύψουμε αυτές τις ανάγκες.

Συνεχίζουμε και σε αυτό το άρθρο, να μας ενδιαφέρει η επίλυση των προβλημάτων χρησιμοποιώντας τεχνικές που αφορούν την ενέργεια (ακουστικά ή ηλεκτρομαγνητικά σήματα).

Παρόλα αυτά, αν μας ενδιαφέρει η χρήση κάμερας και ο εντοπισμός με οπτικές μεθόδους, μπορούμε να συνεχίσουμε την ανάγνωση εδώ.

●─● Γράφοι

Ας ορίσουμε το localization problem με έναν πιο αυστηρό μαθηματικό φορμαλισμό.

Μην τρομάζεις! Δεν θα μπούμε σε λεπτομέρειες! Πιο πολύ θα το κάνουμε για το τυπικό. Ώστε να καταλάβουμε ότι η εύρεση θέσης ενός αντικειμένου μπορεί να μοντελοποιηθεί.

Έστω ότι έχουμε στην διάθεση μας \(n\) αριθμό από nodes, και για λόγους απλότητας - συμμετρικά και όμοια δίκτυα επικοινωνίας - με εμβέλεια \(r\) - για κάθε node.
Συνεπώς, ένα node \(u\) επικοινωνεί με το \(v\) αν και μόνο αν, και το \(v\) μπορεί να επικοινωνήσει πίσω στο \(u\), τα οποία είναι διαρκορπισμένα σε ένα δισδιάστατο τετραγωνικό πεδίο - γίνεται η θεώρηση για δισδιάστατη \(R^2\) ανάλυση - \(Q=[0,s]\times[0,s]\).

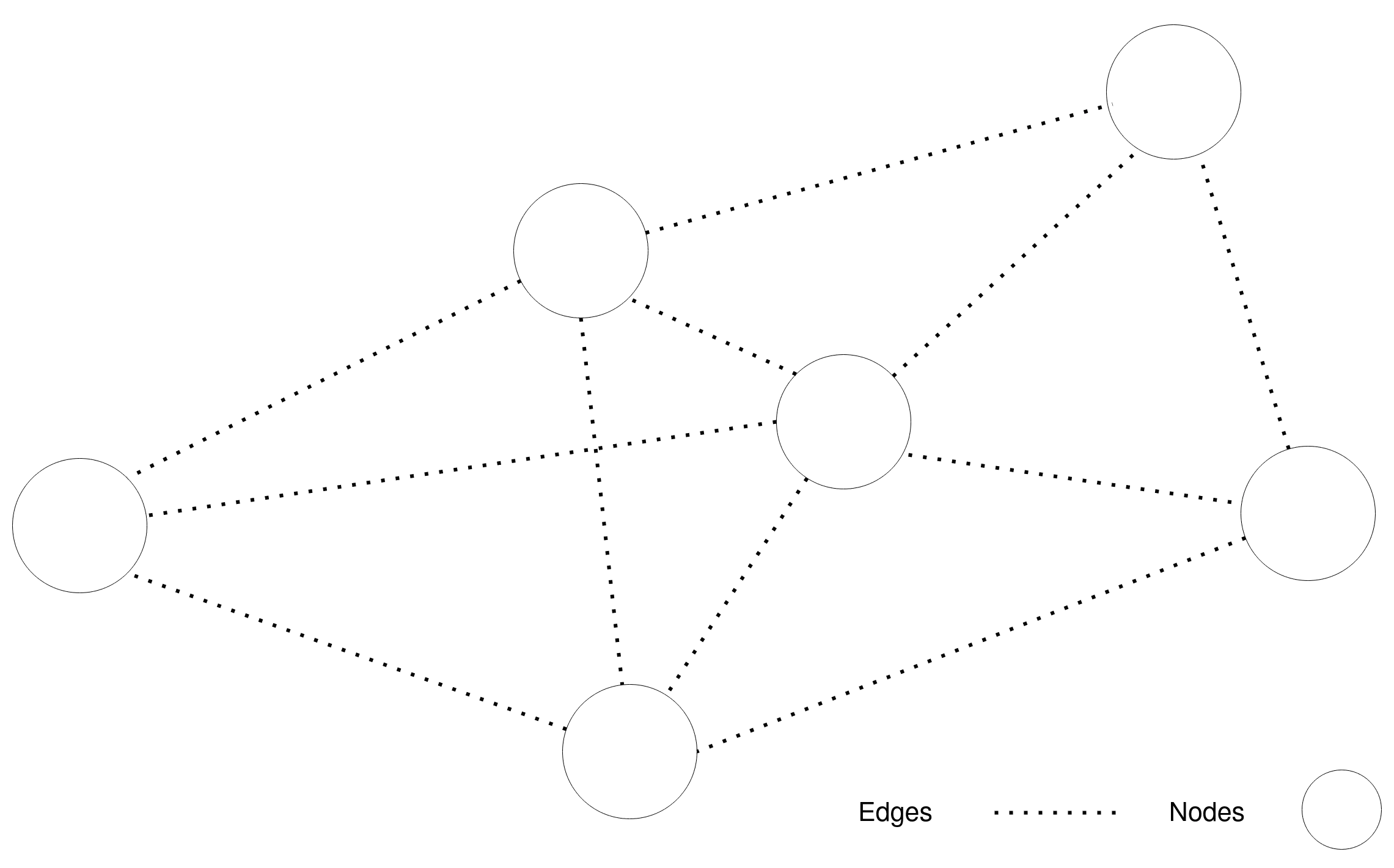
Τότε μπορούμε να μοντελοποιήσουμε το δίκτυο από nodes, ως ένα μη κατευθυνόμενο γράφο \(G = (V, E)\) με τα εξής χαρακτηριστικά:

a. \(V = \{v_1, v_2, ..., v_n\}\) το σύνολο των nodes, όπου έχει την έννοια των κορυφών του γράφου, με \(|V| = n\) *.
b. \(\langle i,j\rangle \in E\) εάν το \(u_i\) μπορεί να επικοινωνήσει με το \(v_i\). Πράγμα που σημαίνει - με βάση τα παραπάνω - ότι η ευκλείδεια απόσταση τους είναι μικρότερη από \(r\) και έχει την έννοια των ακμών του γράφου, με \(|E| = m\) *.
c. \(0 \le w(e) \le r\) με \(e = \langle i,j\rangle\), να είναι το βάρος της κάθε ακμής και να χρησιμοποιείται για την έννοια της απόστασης \(d_{ij}\) μεταξύ του node \(u_i\) με το \(v_i\).

* Ο συμβολισμός || χρησιμοποιείται για να υποδηλώσει το cardinality του εκάστοτε set.

Πάμε τώρα σε απλά λόγια…

Το πρόβλημα εντοπισμού της θέσης δεν είναι τίποτα άλλο παρά ένα πρόβλημα γράφων, που για κάποιους κόμβους αυτού του δικτύου ξέρουμε την θέση τους, ενώ για κάποιους άλλους δεν την γνωρίζουμε και ψάχουμε να την βρούμε.

Αυτό κράτα!

Τώρα, για τα μαθηματικά… Ας τα αφήσουμε απλά να υπάρχουν και, αν ποτέ χρειαστούν, τότε ίσως τα αναλύσουμε σε κάποιο άλλο άρθρο.

Αφού έχουμε ορίσει το πρόβλημα χρησιμοποιώντας γράφους, τώρα πλέον είμαστε σε θέση να μπορούμε να χρησιμοποιήσουμε τις τεχνικές που θα αναλύσουμε παρακάτω για να λύσουμε το πρόβλημα.

🗒 One-hop vs Multi-hop

Η πρώτη κατηγοριοποίηση στην οποία θα αναφερθούμε προκειμένου να εκτιμήσουμε την θέση των nodes είναι από ποιους κόμβους τελικά θα αξιοποιήσουμε πληροφορία.

Στους αλγόριθμους One-hop αξιοποιείται πληροφορία μόνο από άμεσους γείτονες των nodes, προκειμένου να υπολογίσουμε την θέση του κόμβου στο χώρο.

Αντίθετα, στις τεχνικές Multi-hop χρησιμοποιούμε και πληροφορία που λαμβάνουμε έμμεσα – από τους γείτονες των γειτόνων μας – προκειμένου να αποφανθούμε για την θέση ενός node.

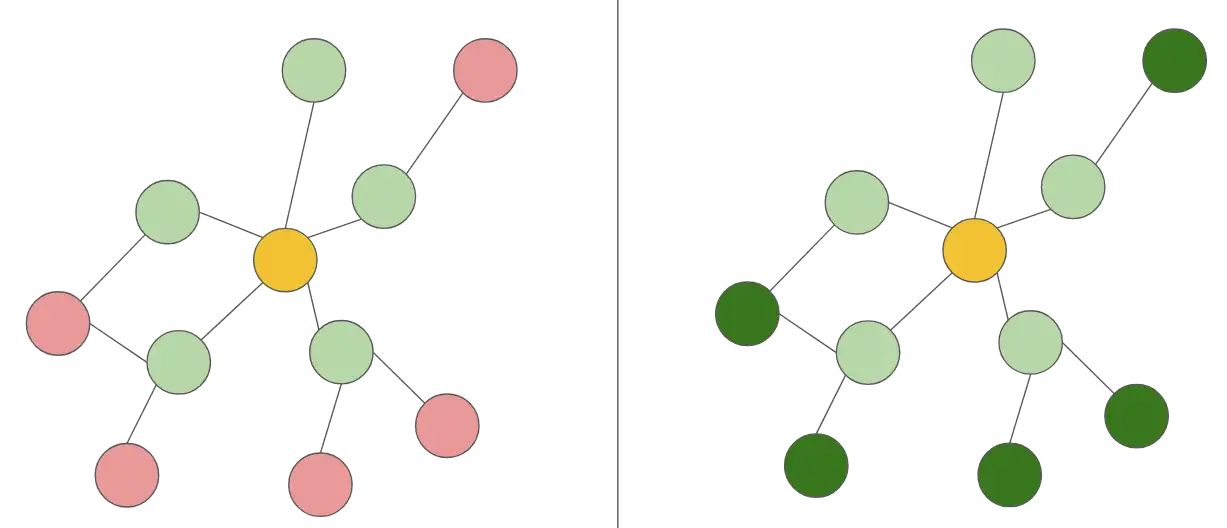
Στην παραπάνω εικόνα, έστω ότι θέλουμε να βρούμε πού βρίσκεται στον χώρο ο κίτρινος κόμβος. Με ελαφρύ πράσινο σημειώνονται οι άμεσοι γείτονές του, ενώ, ανάλογα με την προσέγγιση που θα ακολουθήσουμε, είτε δεν θα χρησιμοποιήσουμε άλλους κόμβους (κόκκινο χρώμα για one-hop) είτε θα χρησιμοποιήσουμε και γείτονες γειτόνων (σκούρο πράσινο για multi-hop).

🗒 Anchor-based vs Anchor-free

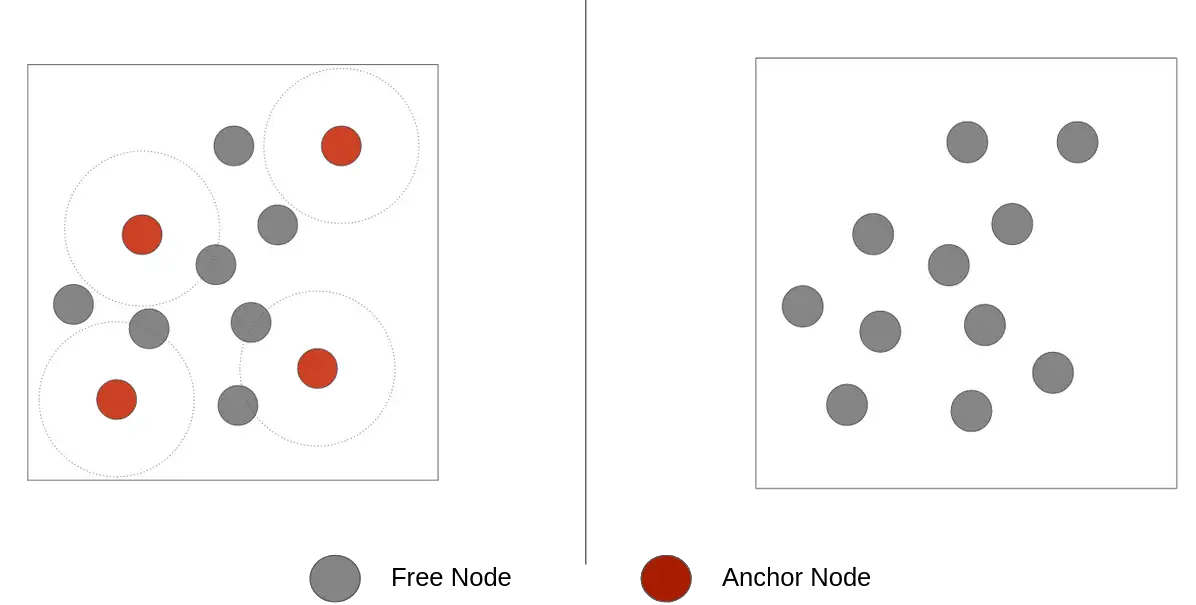
Ένας ακόμα σημαντικός διαχωρισμός αφορά την ύπαρξη ή όχι στο δίκτυο από anchor nodes.

Τα anchor nodes ή αλλιώς beacons είναι αυτά για τα οποία γνωρίζουμε ήδη τη θέση τους – φαντάσου τα σαν είναι σημεία αναφοράς.

Και παρόλο που στην αρχή υποδειλώσαμε ότι είναι αναγκαίο να έχουμε τέτοιους κόμβους.

Εεε… Δες..

Στην πραγματικότητα δεν είναι απόλυτη ανάγκη… Μπορούμε ακόμα και χωρίς την ύπαρξη τέτοιων κόμβων να υπολογίσουμε τη θέση συσκευών.

Καθώς υπάρχουν εφαρμογές στις οποίες μπορεί να μην χρειάζεται ή να μην έχουμε τη δυνατότητα να τοποθετήσουμε beacons (ακόμα και αν αναφερόμαστε σε mobile beacons) τότε θα χρησιμοποιήσουμε anchor-free αλγορίθμους. Αν υπάρχει η δυνατότητα χρήσης τους, τότε ενδιαφερόμαστε για anchor-based μεθόδους.

🗒 Relative vs Absolute Positioning

Ανάλογα με τις προδιαγραφές της εφαρμογής που θέλουμε να καλύψουμε, θα πρέπει να χρησιμοποιήσουμε ανάλογες τεχνικές εκτίμησης θέσης.

Υπάρχουν εφαρμογές, όπως για παράδειγμα η εκτίμηση θέσεων των nodes ενός κινούμενου swarm για χαρτογράφηση σε άγνωστο terrain.

Σε αυτού του τύπου τις εφαρμογές, μας ενδιαφέρει η απόλυτη θέση στον χώρο –οπότε θέλουμε μεθοδολογίες για Absolute Positioning, ενώ υπάρχουν άλλες εφαρμογές στις οποίες μας ενδιαφέρει μόνο η πληροφορία θέσεων σε σχέση με τα υπόλοιπα στοιχεία του περιβάλλοντος της εφαρμογής, οπότε χρειαζόμαστε Relative Positioning.

🗒 Indoor vs Outdoor Scenarios

Κάτι ακόμα που πρέπει να προσέξουμε είναι το περιβάλλον στο οποίο θα βρίσκεται η εφαρμογή, καθώς ανάλογα με το περιβάλλον έχουμε να διαχειριστούμε και τις δυσκολίες που παρουσιάζει – εμπόδια, ανακλάσεις σημάτων κ.λπ.

Δύο κύριοι διαχωρισμοί είναι τα Indoor Scenarios και τα Outdoor Scenarios.

🗒 Distributed vs Centralized Position Computation

Πρέπει να αναφερθεί επίσης ότι είναι πολύ σημαντικό να είναι ξεκάθαρο το σημείο στο οποίο θα γίνεται η επεξεργασία της πληροφορίας.

Υπάρχουν δύο ενδεχόμενα. Το πρώτο είναι ένας σταθμός βάσης (Base Station) να αντιλαμβάνεται και να υπολογίζει την θέση των nodes, τα οποία έπειτα θα ενημερώνονται μέσω αυτού για τη θέση τους – οπότε τότε αναφερόμαστε σε Centralized τεχνικές.

Αντίθετα, άλλη εναλλακτική είναι να γίνει η επεξεργασία τοπικά.

Σε αυτήν την περίπτωση, αναφερόμαστε σε Decentralized ή Distributed αλγορίθμους – όπου κάθε node επικοινωνεί με τα γειτονικά του για την απόκτηση πληροφορίας και έπειτα υπολογίζει μεμονωμένα τη θέση του.

Το μεγάλο πλεονέκτημα των Centralized αλγορίθμων είναι ότι απομακρύνουμε το πρόβλημα του computation από κάθε node. Ωστόσο, προκύπτουν δυσκολίες όπως καθυστερήσεις στις επικοινωνίες, μεγαλύτερη κατανάλωση ενέργειας και εύρους ζώνης, ενώ τέλος και προβλήματα με το scalability του συστήματος – καθώς προτείνονται κυρίως για μικρότερα δίκτυα. Αυτό, όμως, σε κάποιο βαθμό μπορεί να λυθεί με τη χρήση πολλαπλών BS, δημιουργώντας ένα multi-tier network.

Γνωστοί Centralized αλγόριθμοι είναι ο Multi Dimensional Scaling-Mobile Assisted Programming (MDS-MAP), το Semi Definite Programming (SDP) και το Localization Based on Simulated Annealing (LBSA).

🗒 Range-based vs Range-free

Όσον αφορά τους Energy-based, αναλύθηκαν σε άλλα άρθρα τεχνικές εκτίμησης απόστασης ή γωνίας μεταξύ των nodes - συγκεκριμένα οι RSSI, ToA, TDoA και AoA.

Σε αυτήν την περίπτωση, όταν χρησιμοποιούμε δηλαδή έξτρα hardware ή γενικά εκτεταμένες ranging τεχνικές για να καταλήξουμε στις θέσεις των free nodes στον χώρο, αναφερόμαστε σε Range-based μεθόδους.

Θετικό σε αυτήν την περίπτωση είναι ότι έχουμε μεγαλύτερη ακρίβεια της θέσης, όμως ταυτόχρονα πιθανόν να χρειαστούμε ακριβότερα nodes - λόγο των έξτρα components ή του πιο sophisticated hardware.

Για να το αποφύγουμε αυτό, μπορούμε να χρησιμοποιήσουμε τεχνικές οι οποίες ονομάζονται Range-free.

Αυτές οι τεχνικές δεν απαιτούν κανένα επιπρόσθετο hardware, διότι δεν χρησιμοποιούν εκτιμήσεις απόστασης/γωνίας, συνεπώς έχουμε μικρότερο κόστος ανά node.

Έχουν αρκετό ενδιαφέρον λόγω της απλότητας τους παρά την μικρότερη ακρίβεια που παρέχουν. Γνωστοί Range-free αλγόριθμοι είναι ο Approximate Point in Triangle (APIT), Distance Vector-Hop (DV-Hop), Centroid και Gradient.

💭 Σύνοψη

Σε ευρύτερη κλίμακα, στην βιβλιογραφία υπάρχουν επιπλέον αλγόριθμοι ή παραλλαγές χρήσης αυτών που αναφέρθηκαν, για την εύρεση τοποθεσίας nodes σε ένα δίκτυο γράφων. Παρόλα αυτά, σε αυτό το σημείο έγινε μία συνοπτική αναφορά τους, και μία πρώτη ανάλυση γύρω από το localization problem.

Για να συνοψίσουμε…

Το να υπολογίσουμε τη θέση μας, ακόμα και με GPS, δεν είναι εύκολη υπόθεση. Απαιτεί σκέψη, μαθηματικά και έξυπνες τακτικές…

Όπως μάλλον έχει γίνει διακριτό σε αυτή τη σειρά άρθρων, το GPS δεν διαθέτει κάποιο μαγικό μηχανισμό που από μόνος του αντιλαμβάνεται τη θέση μας και μας ενημερώνει.

Τουναντίον!

Είναι ένα πολύπλοκο σύστημα που, ακόμη κι αν γνωρίζουμε τις βασικές του αρχές, προκειμένου να το υλοποιήσουμε στην πράξη, πρέπει να λάβουμε υπόψη και άλλους παράγοντες.

Ακόμα και την ταχύτητα των δορυφόρων, τη θεωρία της σχετικότητας του Αϊνστάιν, τον συγχρονισμό των ατομικών ρολογιών – παράγοντες που πολλές φορές ίσως να μην είχαμε σκεφτεί εξαρχής.

🔗 Παραπομπές

[1] Christos Spyridakis, “Design and implementation of a low cost embedded system for localization of drones flying in swarms”, Diploma Work, School of Electrical and Computer Engineering, Technical University of Crete, Chania, Greece, 2022 https://doi.org/10.26233/heallink.tuc.91531 [2] S. P. Singh and S. Sharma, “Range free localization techniques in wireless sensor networks: A review,” Procedia Computer Science, vol. 57, pp. 7 –16, 2015, 3rd International Conference on Recent Trends in Computing 2015 (ICRTC-2015), issn: 1877-0509. doi: https://doi.org/10.1016/j.procs.2015.07.357. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1877050915018864. [3] C. Zhou, T. Xu, and H. Dong, “Distributed locating algorithm mds-map (lf) based on low-frequency signal,” Computer Science and Information Systems, vol. 12, pp. 55–55, Nov. 2015. doi: 10.2298/CSIS140801055Z. [4] X. Wang and N. Yunfeng, “An improved distance vector-hop localization algorithm based on coordinate correction,” International Journal of Distributed Sensor Networks, vol. 13, p. 155 014 771 774 183, Nov. 2017. doi: 10.1177/1550147717741836. [5] X. Yang and W. Zhang, “An improved dv-hop localization algorithm based on hop distance and hops correction,” International Journal of Multimedia and Ubiquitous Engineering, vol. 11, pp. 319–328, Jun. 2016. doi: 10.14257/ijmue.2016.11.6.28. [6] L. Yin, “A new distance vector-hop localization algorithm based on half-measure weighted centroid,” Mobile Information Systems, vol. 2019, pp. 1–9, Jan. 2019. doi: 10.1155/2019/9892512.